por Evaldo » Seg Jan 04, 2010 15:31
por Evaldo » Seg Jan 04, 2010 15:31
Desitos não cheguei ao resutado do gabarito.
Uma urna I contém 2 bolas vermelhas e 3 bolas brancas e outra II, contém 4 bolas vermelhas e 5 bolas brancas. Sorteia-se uma urna e dela retira-se, ao acaso, uma bola. Qual é a probabilidade de que a bola seja vermelhae tenha vindo da urna I.?
Gabarito: 1/5
Jogando-se ao mesmo tempo 2 dados honestos, a probabilidade de a soma dos pontos ser igual a 5 é:
Gabarito: 1/9
Há homens que lutam um dia, e são bons;
Há outros que lutam um ano, e são melhores;
Há aqueles que lutam muitos anos, e são muito bons;
Porém há os que lutam toda a vida
Estes são os imprescindíveis
Bertold Brecht
-
Evaldo
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Qua Out 14, 2009 13:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciências Contábeis
- Andamento: formado
 por MarceloFantini » Seg Jan 04, 2010 15:59
por MarceloFantini » Seg Jan 04, 2010 15:59
Boa tarde Evaldo!
No primeiro problema, como ele não afirmou nada, suponha que a probabildade seja igual para ambas urnas, logo

para cada. Para a urna 1, a probabilidade de ser sorteada a bola vermelha é

. Como ele quer a probabilidade de que a bola sorteada seja da
urna 1 e vermelha, temos:


.
No segundo problema, o espaço amostral tem 36 possibilidades. Contudo, existem apenas
quatro pares que dão soma 5:

. Logo, a probabilidade pedida é:

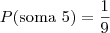
Espero ter ajudado.
Um abraço.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Evaldo » Seg Jan 04, 2010 16:09
por Evaldo » Seg Jan 04, 2010 16:09
Fantini,
Muito obrigado viu, agradeço muito eu fiquei muito errolado nessas duas questões.
Um forte abraço.
Evaldo.
Há homens que lutam um dia, e são bons;
Há outros que lutam um ano, e são melhores;
Há aqueles que lutam muitos anos, e são muito bons;
Porém há os que lutam toda a vida
Estes são os imprescindíveis
Bertold Brecht
-
Evaldo
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Qua Out 14, 2009 13:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciências Contábeis
- Andamento: formado
Voltar para Estatística
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Probabilidade] Exercício Desafio de Probabilidade
por werwer » Qua Mar 21, 2012 18:57
- 0 Respostas
- 10336 Exibições
- Última mensagem por werwer

Qua Mar 21, 2012 18:57
Estatística
-
- Probabilidade - Função Densidade de Probabilidade
por pimgui » Qua Dez 16, 2020 10:53
- 0 Respostas
- 21644 Exibições
- Última mensagem por pimgui

Qua Dez 16, 2020 10:53
Probabilidade
-
- Probabilidade - função probabilidade
por tarlix » Ter Mai 24, 2011 12:41
- 1 Respostas
- 5341 Exibições
- Última mensagem por Neperiano

Dom Out 16, 2011 17:00
Estatística
-
- [Probabilidade] probabilidade de obj com estudantes
por fenixxx » Seg Ago 13, 2012 14:06
- 1 Respostas
- 4516 Exibições
- Última mensagem por Neperiano

Ter Out 09, 2012 10:10
Probabilidade
-
- [probabilidade condicional] probabilidade de gol.
 por Mr_ MasterMind » Sáb Set 19, 2015 17:35
por Mr_ MasterMind » Sáb Set 19, 2015 17:35
- 0 Respostas
- 4530 Exibições
- Última mensagem por Mr_ MasterMind

Sáb Set 19, 2015 17:35
Probabilidade
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 para cada. Para a urna 1, a probabilidade de ser sorteada a bola vermelha é
para cada. Para a urna 1, a probabilidade de ser sorteada a bola vermelha é  . Como ele quer a probabilidade de que a bola sorteada seja da
. Como ele quer a probabilidade de que a bola sorteada seja da 
 .
. . Logo, a probabilidade pedida é:
. Logo, a probabilidade pedida é: