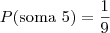### Probabilidade ###

por **Evaldo** » Seg Jan 04, 2010 15:31

Desitos não cheguei ao resutado do gabarito.

Uma urna I contém 2 bolas vermelhas e 3 bolas brancas e outra II, contém 4 bolas vermelhas e 5 bolas brancas. Sorteia-se uma urna e dela retira-se, ao acaso, uma bola. Qual é a probabilidade de que a bola seja vermelhae tenha vindo da urna I.?

Gabarito: 1/5

Jogando-se ao mesmo tempo 2 dados honestos, a probabilidade de a soma dos pontos ser igual a 5 é:

Gabarito: 1/9

por **MarceloFantini** » Seg Jan 04, 2010 15:59

Boa tarde Evaldo!

No primeiro problema, como ele não afirmou nada, suponha que a probabildade seja igual para ambas urnas, logo $\frac{1}{2}$ para cada. Para a urna 1, a probabilidade de ser sorteada a bola vermelha é $\frac{2}{5}$ . Como ele quer a probabilidade de que a bola sorteada seja da urna 1 e vermelha, temos:

$P(\mbox{urna 1 e vermelha}) = \frac{1}{2} \times \frac{2}{5}$

$P(\mbox{urna 1 e vermelha}) = \frac{1}{5}$ .

No segundo problema, o espaço amostral tem 36 possibilidades. Contudo, existem apenas quatro pares que dão soma 5: (1,4); (2,3); (3,2); (4,1)

. Logo, a probabilidade pedida é:

$P(\mbox{soma 5})=\frac{4}{36}$

$P(\mbox {soma 5})=\frac{1}{9}$

Espero ter ajudado.

Um abraço.

por **Evaldo** » Seg Jan 04, 2010 16:09

Fantini,
Muito obrigado viu, agradeço muito eu fiquei muito errolado nessas duas questões.
Um forte abraço.
Evaldo.

### Probabilidade ###

### Probabilidade ###

### Probabilidade ###

Re: ### Probabilidade ###

Re: ### Probabilidade ###

Quem está online