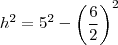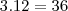por slade » Dom Out 13, 2013 15:15
por slade » Dom Out 13, 2013 15:15
A aresta lateral de uma pirâmide triangular regular mede 5 m, e a aresta da base, 6 m. A área lateral dessa pirâmide, em m^2, é

resposta=36
-
slade
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Dom Out 13, 2013 15:11
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por young_jedi » Ter Out 15, 2013 19:38
por young_jedi » Ter Out 15, 2013 19:38
por teorema de pitagoras encontramos a altura dos triangulos das faces
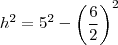

então a area de cada face sera

vezes as tres faces
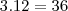
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por slade » Ter Out 15, 2013 20:09
por slade » Ter Out 15, 2013 20:09
cara o apótema da base seria a metade da aresta do triangulo?
-
slade
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Dom Out 13, 2013 15:11
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por young_jedi » Ter Out 15, 2013 21:14
por young_jedi » Ter Out 15, 2013 21:14
os triangulos das faces tem um lado igual ao lada da base ou seja igual a 6 e os outros dois lados são iguais a 5
portanto é um triangulo isoceles e sua altura é calculada pelo teorema de pitagoras

- tirang.png (1.59 KiB) Exibido 2224 vezes
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Area lateral?
por bmachado » Sáb Jun 23, 2012 17:09
- 2 Respostas
- 2524 Exibições
- Última mensagem por bmachado

Dom Jun 24, 2012 12:11
Geometria Espacial
-
- [tronco de cone / área lateral] geometrial espacial
por sandra silva » Ter Ago 26, 2008 22:08
- 2 Respostas
- 7120 Exibições
- Última mensagem por sandra silva

Qua Ago 27, 2008 07:34
Geometria Espacial
-
- [Geometria Espacial - Pirâmide] Pirâmide de Cartolina
por raimundoocjr » Qui Ago 02, 2012 22:13
- 1 Respostas
- 2695 Exibições
- Última mensagem por MarceloFantini

Qui Ago 02, 2012 23:04
Geometria Espacial
-
- limite lateral
por Nina » Qua Out 21, 2009 18:25
- 2 Respostas
- 2966 Exibições
- Última mensagem por MarceloFantini

Ter Set 21, 2010 20:18
Cálculo
-
- [Limite] Lateral
por eli83 » Ter Out 09, 2012 11:15
- 4 Respostas
- 2554 Exibições
- Última mensagem por eli83

Qua Out 10, 2012 00:21
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.