Olá. Estou no primeiro ano do curso de matemática e ainda não estudei a parte de probabilidade, mas vou apresentar uma resolução que remete ao que ainda lembro do ensino médio. Se você tem o gabarito, por favor coloque a resposta e certa; e desculpe se a minha resposta estiver errada, porém tenho quase certeza de que é assim:
Observe que quando jogamos dois dados simultaneamente, temos 36 possibilidades, ou seja:
1 2 3 4 5 6
1
2 3 4 5 6 72
3 4 5 6 7 83
4 5 6 7 8 94
5 6 7 8 9 105
6 7 8 9 10 116
7 8 9 10 11 12É como uma tabela na qual você consegue visualizar as possibilidades. Por exemplo: temos o dado A e o dado B; se o dado A apresenta, na jogada, o número 1, então, este número virá acompanhado pelo número do dado B, que pode ser 1, 2, 3, 4, 5 ou 6. Daí pode ser: 1+1, 1+2, 1+3, 1+4, 1+5, 1+6.
O mesmo ocorre com as outras faces do dado, totalizando, assim, 36 possibilidades.
Bom, prosseguindo, temos a "regra do ou", na qual somamos as possibilidades e é o que iremos usar aqui.
Assim, a questão pergunta qual é a possibilidade de adquirirmos uma soma tal que seja um número ímpar OU um número
menor que 10.
Então:
Observe que a possibilidade de obtermos um número ímpar é de
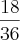
, pois temos 18 possíveis números ímpares em 36 possibilidades (estão sublinhados na "tabela" acima). Veja, agora, que a possibilidade de obtermos um número menor que 10 é de
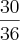
, pois note que temos apenas 6 possíveis números maiores do que 6 e, portanto, 30 menores do que 6.
Assim, aplicando a "regra do ou":

(Desculpa se está errado! Envie a resposta correta, por favor).
Talvez você possa ter errado na hora de simplificar as frações.
Até mais.


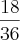 , pois temos 18 possíveis números ímpares em 36 possibilidades (estão sublinhados na "tabela" acima). Veja, agora, que a possibilidade de obtermos um número menor que 10 é de
, pois temos 18 possíveis números ímpares em 36 possibilidades (estão sublinhados na "tabela" acima). Veja, agora, que a possibilidade de obtermos um número menor que 10 é de 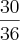 , pois note que temos apenas 6 possíveis números maiores do que 6 e, portanto, 30 menores do que 6.
, pois note que temos apenas 6 possíveis números maiores do que 6 e, portanto, 30 menores do que 6.

![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.