Existe outra maneira de responder esse problema?
A resposta correta foi dada por um amigo português que gentilmente fez esse vídeo:
http://www.youtube.com/watch?v=H4kdxUJVWDY
Agora vem a sacada de que

por que para que

,

e

sejam uma PA progressiva a diferença de cada termo um pelo outro imediatamente anterior deve ser igual a razão, ou seja,

deve ser a razão, ou seja,

é igual a

mais a razão que é

. Nesse caso nós temos

que é

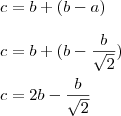
Agora temos que racionalizar a raiz para que ela fique no numerador. Os professores, em geral, preferem as raízes no numerador. E quando eles fazem concursos fazem alternativas equivalentes que mostrem a resposta final com as raízes no numerador, eu suponho.
Racionalizando:

A alternativa correta é a resposta e): que aparece como
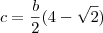
, que é o mesmo que a resposta final, basta multiplicar.
 ,
,  e
e  constantes reais com
constantes reais com  formando, nesta ordem, uma progressão aritmética e tais que a soma das raízes da equação
formando, nesta ordem, uma progressão aritmética e tais que a soma das raízes da equação 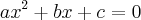 é
é  . Então uma relação válida entre
. Então uma relação válida entre  e
e  é:
é:
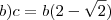

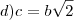

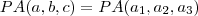
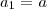


 e
e  na equação:
na equação: 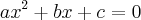 :
:
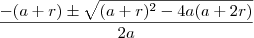

 e
e  .
.

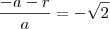
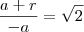

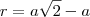


 por que para que
por que para que  deve ser a razão, ou seja,
deve ser a razão, ou seja,  . Nesse caso nós temos
. Nesse caso nós temos 
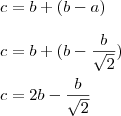

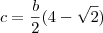 , que é o mesmo que a resposta final, basta multiplicar.
, que é o mesmo que a resposta final, basta multiplicar.
 .
.



