 por Eduardo_GNR » Qui Mar 14, 2013 21:41
por Eduardo_GNR » Qui Mar 14, 2013 21:41
Pessoal,
Sou novo no fórum e estou estudando funções injetoras, sobrejetoras, bijetoras, enfim, e tenho 3 exercícios aqui que eu não sei como fazer. Alguém ajuda?
Determine quais das seguintes funções de Z ? Z são injetoras:
1 f(x) = x ? 1 2 f(x) = x2 + 1 3 f(x) = dx/2e
2 Quais das funções anteriores são sobrejetoras? 3 Se f e f ? g são injetoras, então g é injetora também? Apresente uma prova para justi?car a sua resposta
Obrigado.
-
Eduardo_GNR
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Qui Mar 14, 2013 21:37
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciência da Computação
- Andamento: cursando
 por e8group » Sex Mar 15, 2013 12:15
por e8group » Sex Mar 15, 2013 12:15
vou postar apenas a resolução (2) não entendi a questão (1) não estar claro ,por isso é importante utilizar LaTeX para redigir suas equações ,fórmulas e etc .
Resolução : (Caso geral )
Considere ,

e
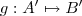
.
Hipótese :
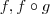
são injectivas .
Vamos considerar o caso em que
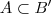
mas

não está contido em

.Sendo assim ,

e

.
Suponhamos que

não é injectiva ,isto é , dados
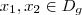
distintos não implica

,em outras palavras ,dados
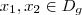
distintos ,podemos ter

.Se
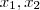
são simultaneamente elementos do conjunto

e

,isto é ,

então

é injetiva .
Prova :
Como estamos supondo que

não é injectiva , podemos ter

para

.Se

então

, por outro lado
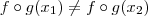
para

.
Observe que temos uma contradição , pois
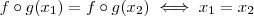
;logo

é injetiva .
Deixo para você o caso em que

ou seja

e
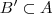
o argumento será semelhante .
Espero que ajude .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Função injetora, sobrejetora.. par, ímpar?
por Jonatan » Sex Jul 30, 2010 11:59
- 1 Respostas
- 2077 Exibições
- Última mensagem por MarceloFantini

Sex Jul 30, 2010 15:08
Funções
-
- função injetora
por lineleal18 » Seg Nov 02, 2009 14:13
- 1 Respostas
- 6004 Exibições
- Última mensagem por thadeu

Qua Nov 04, 2009 13:09
Funções
-
- Função injetora
por Pri Ferreira » Qua Nov 09, 2011 20:52
- 1 Respostas
- 1046 Exibições
- Última mensagem por LuizAquino

Qui Nov 10, 2011 20:19
Funções
-
- Função não sobrejetora
por Cleyson007 » Ter Abr 24, 2012 09:50
- 3 Respostas
- 2866 Exibições
- Última mensagem por Russman

Ter Abr 24, 2012 16:50
Funções
-
- Função sobrejetora
por leandrofontesantos » Seg Set 29, 2014 13:08
- 3 Respostas
- 1721 Exibições
- Última mensagem por adauto martins

Sáb Out 04, 2014 12:22
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 e
e 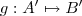 .
. 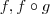 são injectivas .
são injectivas .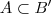 mas
mas  não está contido em
não está contido em  .Sendo assim ,
.Sendo assim , e
e  .
.  não é injectiva ,isto é , dados
não é injectiva ,isto é , dados 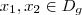 distintos não implica
distintos não implica  ,em outras palavras ,dados
,em outras palavras ,dados  .Se
.Se 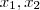 são simultaneamente elementos do conjunto
são simultaneamente elementos do conjunto  ,isto é ,
,isto é ,  então
então  .Se
.Se  , por outro lado
, por outro lado 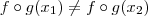 para
para 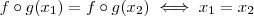 ;logo
;logo  ou seja
ou seja  e
e 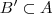 o argumento será semelhante .
o argumento será semelhante . 