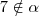por Zanatta » Ter Mar 05, 2013 18:37
por Zanatta » Ter Mar 05, 2013 18:37
Olá, tentei ler a teoria pelo liro e fiquei meio confuso, acabei nao conseguindo resolver esse exercicio, quem puder me ajudar:
É numero real ? Justifique sua resposta.
a(alfa) = {p E(pertence) Q | 3p + 1< 2p - 5}
quem puder me ajudar, grato desde já.
-
Zanatta
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Ter Mar 05, 2013 18:21
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Estatistica
- Andamento: cursando
 por e8group » Qua Mar 06, 2013 10:32
por e8group » Qua Mar 06, 2013 10:32
Definição :
Um número real é um subconjunto

,de números racionais ,que satisfaz 4 propriedades .
(1) Se

e

é um número racional com
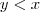
,então
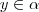
.
(2)

(3)
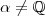
(4)

não tem máximo , em outras palavras ,se

,então existe algum

em

com
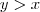
.
Solução :
Dado o subconjunto

,temos :
(1) Sejam

racionais quaisquer , com

e
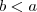
,temos :

.
Como
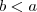
,segue

implica que

(2)

(é fácil ver !) ,

(3)
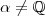
,pois,

e
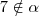
Deixo para você desenvolver a propriedade (4) e concluir o exercício .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por e8group » Qua Mar 06, 2013 10:33
por e8group » Qua Mar 06, 2013 10:33
Definição :
Um número real é um subconjunto

,de números racionais ,que satisfaz 4 propriedades .
(1) Se

e

é um número racional com
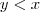
,então
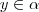
.
(2)

(3)
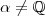
(4)

não tem máximo , em outras palavras ,se

,então existe algum

em

com
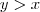
.
Solução :
Dado o subconjunto

,temos :
(1) Sejam

racionais quaisquer , com

e
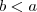
,temos :

.
Como
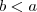
,segue

implica que

(2)

(é fácil ver !) ,

(3)
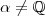
,pois,

e
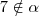
Deixo para você desenvolver a propriedade (4) e concluir o exercício .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Conjuntos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Módulo de um Número real
 por gustavoluiss » Sáb Fev 26, 2011 00:58
por gustavoluiss » Sáb Fev 26, 2011 00:58
- 1 Respostas
- 2381 Exibições
- Última mensagem por LuizAquino

Sáb Fev 26, 2011 11:37
Funções
-
- [numero real] Restrição ao Denominador
por cacau cracco » Qui Mai 24, 2012 20:11
- 1 Respostas
- 4009 Exibições
- Última mensagem por fraol

Sáb Mai 26, 2012 00:19
Álgebra Elementar
-
- [condição para ser um número real]
por JKS » Qui Jun 20, 2013 01:16
- 0 Respostas
- 1159 Exibições
- Última mensagem por JKS

Qui Jun 20, 2013 01:16
Números Complexos
-
- Função real de variável real!
por kellykcl » Qui Mai 01, 2014 13:41
- 2 Respostas
- 3267 Exibições
- Última mensagem por kellykcl

Qui Mai 01, 2014 16:28
Funções
-
- função real
por cristina » Seg Abr 19, 2010 23:54
- 2 Respostas
- 2159 Exibições
- Última mensagem por MarceloFantini

Ter Abr 20, 2010 19:43
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 ,de números racionais ,que satisfaz 4 propriedades .
,de números racionais ,que satisfaz 4 propriedades . e
e  é um número racional com
é um número racional com 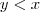 ,então
,então 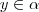 .
. 
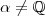
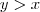 .
. ,temos :
,temos :  racionais quaisquer , com
racionais quaisquer , com  e
e 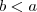 ,temos :
,temos : .
.  implica que
implica que 

 e
e