 por Douglas2013 » Seg Mar 04, 2013 20:11
por Douglas2013 » Seg Mar 04, 2013 20:11
Olá pessoal, estou com uma dúvida.
Enunciado: Dados dois números x e y reais e positivos, chama-se média aritmética de x com y o real a=
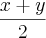
e chama-se média geométrica o real g=
![\sqrt[]{xy} \sqrt[]{xy}](/latexrender/pictures/73a3f5eb9b695f3c2c1b554a600498a8.png)
. Mostre que a

g para todos x , y


positivo.
Eu comecei a responder da seguinte maneira: considerei um numero K, tal que k=xy. Ai fiz :
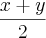

![\sqrt[]{xy} \sqrt[]{xy}](/latexrender/pictures/73a3f5eb9b695f3c2c1b554a600498a8.png)
----------------------


![({\sqrt[]{xy}})^{2} ({\sqrt[]{xy}})^{2}](/latexrender/pictures/e549db8f4d1c9c9f7de7c786769a14a6.png)
----------------
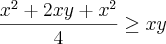
e como k=xy ficou

. Porém eu fiquei estagnado nessa parte, não sei se é porque minha solução esta errada ou por eu estar esquecendo algo ou não sei mais o que. O fato é que fiquei tentando resolver esse problema por mais ou menos 105 minutos até chegar nessa solução. Porém não sei se ela esta certa. Por favor, ajudem -me.
-
Douglas2013
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Sáb Mar 02, 2013 11:27
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por e8group » Seg Mar 04, 2013 20:42
por e8group » Seg Mar 04, 2013 20:42
Pense assim , claramente

;somando-se

na desigualdade ,
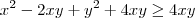
(que também é verdade) .
Como
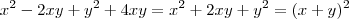
,resulta
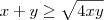
e portanto
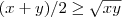
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Douglas2013 » Ter Mar 05, 2013 16:04
por Douglas2013 » Ter Mar 05, 2013 16:04
santhiago escreveu:Pense assim , claramente

;somando-se

na desigualdade ,
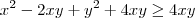
(que também é verdade) .
Como
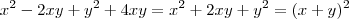
,resulta
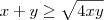
e portanto
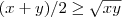
Eu entendi o que tu fez, porém não entendi porque tu iniciiou a demonstração pelo quadrado da diferença. poderia me explicar?
-
Douglas2013
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Sáb Mar 02, 2013 11:27
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Conjuntos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Conjuntos numéricos
por Marcampucio » Ter Set 01, 2009 21:50
- 1 Respostas
- 1440 Exibições
- Última mensagem por Elcioschin

Ter Set 01, 2009 22:38
Álgebra Elementar
-
- Conjuntos numericos
por cristina » Seg Set 14, 2009 18:41
- 1 Respostas
- 1622 Exibições
- Última mensagem por Molina

Ter Set 15, 2009 16:07
Álgebra Elementar
-
- CONJUNTOS NUMÉRICOS
por shallon » Qua Out 28, 2009 23:38
- 0 Respostas
- 1213 Exibições
- Última mensagem por shallon

Qua Out 28, 2009 23:38
Álgebra Elementar
-
- CONJUNTOS NUMÉRICOS
por shallon » Qua Out 28, 2009 23:40
- 0 Respostas
- 1249 Exibições
- Última mensagem por shallon

Qua Out 28, 2009 23:40
Álgebra Elementar
-
- CONJUNTOS NUMÉRICOS
por shallon » Qua Out 28, 2009 23:42
- 0 Respostas
- 1049 Exibições
- Última mensagem por shallon

Qua Out 28, 2009 23:42
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
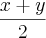 e chama-se média geométrica o real g=
e chama-se média geométrica o real g=![\sqrt[]{xy} \sqrt[]{xy}](/latexrender/pictures/73a3f5eb9b695f3c2c1b554a600498a8.png) . Mostre que a
. Mostre que a g para todos x , y
g para todos x , y
 positivo.
positivo.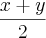

![\sqrt[]{xy} \sqrt[]{xy}](/latexrender/pictures/73a3f5eb9b695f3c2c1b554a600498a8.png) ----------------------
---------------------- 

![({\sqrt[]{xy}})^{2} ({\sqrt[]{xy}})^{2}](/latexrender/pictures/e549db8f4d1c9c9f7de7c786769a14a6.png) ----------------
----------------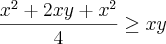 e como k=xy ficou
e como k=xy ficou  . Porém eu fiquei estagnado nessa parte, não sei se é porque minha solução esta errada ou por eu estar esquecendo algo ou não sei mais o que. O fato é que fiquei tentando resolver esse problema por mais ou menos 105 minutos até chegar nessa solução. Porém não sei se ela esta certa. Por favor, ajudem -me.
. Porém eu fiquei estagnado nessa parte, não sei se é porque minha solução esta errada ou por eu estar esquecendo algo ou não sei mais o que. O fato é que fiquei tentando resolver esse problema por mais ou menos 105 minutos até chegar nessa solução. Porém não sei se ela esta certa. Por favor, ajudem -me.

 ;somando-se
;somando-se  na desigualdade ,
na desigualdade ,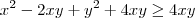 (que também é verdade) .
(que também é verdade) . 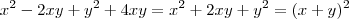 ,resulta
,resulta 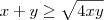 e portanto
e portanto 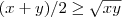

 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
