Aqui eu tive basten dificuldade. Primeiro eu entendo que a ordem não importa nessa situação, uma vez que tanto faz a ordem que as bolas sejam sorteadas, o importante é que no FINAL do sorteio as bolas formem números consecutivos.
Por exemplo, se sair primeiro a bola 5, depois, 7, 4 ,3 6 tudo bem, pois no final teremos (3,4,5,6,7). Ou seja, cinco bolas numeradas consecutivamente no final do sorteio.
Então eu calculei a combinação C100,5 =
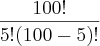que correponde ao número total de sorteios possíveis.Porém, quebrei a cabeça pra conseguir determinar como sortear e sair em ordem. Alguém tem alguma ideia de como fazer?
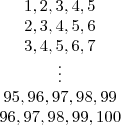
