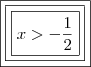por Diofanto » Dom Fev 03, 2013 19:55
por Diofanto » Dom Fev 03, 2013 19:55
A inequação é a seguinte:

Tentei fazer assim:
1º:

O que resultou em

2ª:

O que resultou em

Tenho o gabarito:

O problema é que não consigo fazer a intersecção para chegar na resposta final, e nao tenho certeza se meus cálculos estão corretos.
" A Matemática é o alfabeto com o qual Deus fez o Universo"
-

Diofanto
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Qui Set 20, 2012 15:39
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura e Bacharelado em Matemática
- Andamento: cursando
-
 por DanielFerreira » Dom Fev 03, 2013 20:55
por DanielFerreira » Dom Fev 03, 2013 20:55
Diofanto,
boa noite!
Resolvendo por partes...
I:
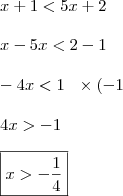
II:

Estudando os sinais:
___-____(- 1/4)
____+_____________+______________-______________-______(+ 1)___+___________
___+____(- 1/4)
____-______(+ 1)___+___________
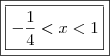
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por Diofanto » Dom Fev 03, 2013 21:46
por Diofanto » Dom Fev 03, 2013 21:46
danjr5,
Era essa dúvida mesmo. A resposta que tenho está errada apenas por um " menos igual".
Obrigado pela ajuda.
" A Matemática é o alfabeto com o qual Deus fez o Universo"
-

Diofanto
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Qui Set 20, 2012 15:39
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura e Bacharelado em Matemática
- Andamento: cursando
-
 por DanielFerreira » Dom Fev 10, 2013 21:41
por DanielFerreira » Dom Fev 10, 2013 21:41
Não há de quê!
Até a próxima!
Daniel.
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por Diofanto » Ter Fev 12, 2013 23:03
por Diofanto » Ter Fev 12, 2013 23:03
Preciso de ajuda com Inequações do segundo Grau:
O sistema é o seguinte:
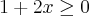

Eu até que resolvi, mas não bate com a minha folha de respostas
Aqui diz que a resposta é:
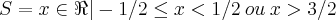
Minha resposta deu:

Quero saber Qual a resposta correta. Eu sei que eu erro muito na hora de fazer a união ou a intersecção.
" A Matemática é o alfabeto com o qual Deus fez o Universo"
-

Diofanto
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Qui Set 20, 2012 15:39
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura e Bacharelado em Matemática
- Andamento: cursando
-
 por e8group » Qua Fev 13, 2013 00:47
por e8group » Qua Fev 13, 2013 00:47
Vou chamar de

o conjunto constituído de todos elementos que satisfaz a primeira inequação ,e de

o conjunto constituído de todos elementos que satisfaz a segunda inequação estrita.A solução do sistema será um subconjunto que estar contido em

e

ao mesmo tempo.
Note que ,

, ok ?
Já para ,

.
Retirando o módulo ,via definição
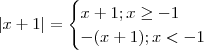
.
Voltamos então onde paramos .
A pergunta é :
(i) Existe algum x em

para que

?
(ii) Existe algum x em
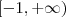
para que
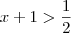
?
Para responder isto ,
(i)

. Portanto ,existe x em

:

, na verdade

satisfaz a nossa pergunta .
(ii)

Certo ?
Concluímos então que

Logo , o conjunto solução do sistema é :

Não sei onde errei ,se errei ... Espero que ajude .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por DanielFerreira » Qui Fev 14, 2013 23:37
por DanielFerreira » Qui Fev 14, 2013 23:37
Diofanto,
boa noite!
Abra um tópico por questão, ok?!
Só para confirmar a resposta do
Santhiago!!
Equação I:
 Equação II
Equação II:

Estudando os sinais da eq. II,

Enfim, a intersecção...
___-________-__________(+ 1/2)
_____+______________-___(- 1/3)_____+___(+ 1/2)
___-______________+___(- 1/3)____-_____(+ 1/2)
___+___________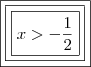
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por Diofanto » Qui Fev 14, 2013 23:45
por Diofanto » Qui Fev 14, 2013 23:45
danjr5, farei isso da próxima vez.
danjr5, Santhiago, Obrigado por tirar as dúvidas. Foi de grande valia.
Grato.
" A Matemática é o alfabeto com o qual Deus fez o Universo"
-

Diofanto
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Qui Set 20, 2012 15:39
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura e Bacharelado em Matemática
- Andamento: cursando
-
Voltar para Inequações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [inequação modular] DÚVIDA SIMPLES EM INEQUAÇÃO MODULAR
por brunocunha2008 » Sex Set 13, 2013 22:37
- 1 Respostas
- 7385 Exibições
- Última mensagem por Rafael Henrique

Qui Jan 03, 2019 14:39
Inequações
-
- Inequação
por Luna » Seg Set 28, 2009 18:55
- 4 Respostas
- 3717 Exibições
- Última mensagem por Molina

Ter Set 29, 2009 16:50
Sistemas de Equações
-
- Inequação
por Luna » Ter Set 29, 2009 16:48
- 1 Respostas
- 2112 Exibições
- Última mensagem por Molina

Qua Set 30, 2009 00:39
Sistemas de Equações
-
- Inequação
por Bebel » Dom Ago 08, 2010 00:50
- 0 Respostas
- 1620 Exibições
- Última mensagem por Bebel

Dom Ago 08, 2010 00:50
Trigonometria
-
- Inequação
por DougMath » Ter Ago 24, 2010 15:41
- 1 Respostas
- 1831 Exibições
- Última mensagem por Molina

Ter Ago 24, 2010 16:45
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.














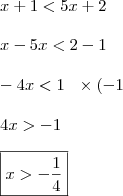

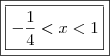



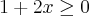

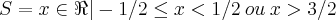


 o conjunto constituído de todos elementos que satisfaz a primeira inequação ,e de
o conjunto constituído de todos elementos que satisfaz a primeira inequação ,e de  o conjunto constituído de todos elementos que satisfaz a segunda inequação estrita.A solução do sistema será um subconjunto que estar contido em
o conjunto constituído de todos elementos que satisfaz a segunda inequação estrita.A solução do sistema será um subconjunto que estar contido em  e
e  ao mesmo tempo.
ao mesmo tempo.  , ok ?
, ok ? .
. 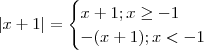 .
.  para que
para que  ?
? 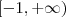 para que
para que 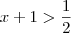 ?
?  . Portanto ,existe x em
. Portanto ,existe x em  :
:  , na verdade
, na verdade  satisfaz a nossa pergunta .
satisfaz a nossa pergunta .  Certo ?
Certo ?