
Tentei fazer assim:
1º:

O que resultou em

2ª:

O que resultou em

Tenho o gabarito:

O problema é que não consigo fazer a intersecção para chegar na resposta final, e nao tenho certeza se meus cálculos estão corretos.








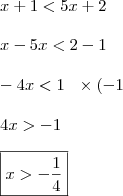

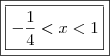



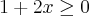

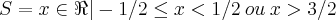


 o conjunto constituído de todos elementos que satisfaz a primeira inequação ,e de
o conjunto constituído de todos elementos que satisfaz a primeira inequação ,e de  o conjunto constituído de todos elementos que satisfaz a segunda inequação estrita.A solução do sistema será um subconjunto que estar contido em
o conjunto constituído de todos elementos que satisfaz a segunda inequação estrita.A solução do sistema será um subconjunto que estar contido em  e
e  ao mesmo tempo.
ao mesmo tempo.  , ok ?
, ok ? .
. 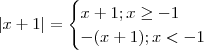 .
.  para que
para que  ?
? 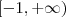 para que
para que 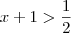 ?
?  . Portanto ,existe x em
. Portanto ,existe x em  :
:  , na verdade
, na verdade  satisfaz a nossa pergunta .
satisfaz a nossa pergunta .  Certo ?
Certo ? 







Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes


 , avisa que eu resolvo.
, avisa que eu resolvo.

