 por sauloandrade » Sáb Dez 29, 2012 21:07
por sauloandrade » Sáb Dez 29, 2012 21:07
Boas pessoal, me deparei com o seguinte problema e não estou conseguindo resolver. Gostaria de pedir a ajuda de vocês para dizer-me onde eu estou errando.
"O Ângulo ADC de um polígono regular ABCDEf...mede 30°.Determine a soma dos ângulos internos desse polígonos.
Então, fiz da seguinte maneira:
Sabemos que Soma dos ângulos internos é:
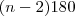
. Sabemos ainda que o polígono é regular então, se eu pegar a soma dos ângulos internos e dividir pelo número de lados eu obterei a medida de cada ângulo interno.

resolvendo teremos
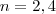
.
Me quebrei ai, pois o n não pertence ao conjunto dos inteiros.
Onde estou errando? ;-;
-
sauloandrade
- Usuário Ativo

-
- Mensagens: 23
- Registrado em: Dom Out 28, 2012 12:03
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por e8group » Dom Dez 30, 2012 11:30
por e8group » Dom Dez 30, 2012 11:30
Bom dia .Há um erro no enunciado ,certo ? Você realmente quer achar a soma dos ângulos ineternos ou apenas obter o valor correspondente a este ângulo interno ?
Se for apenas a soma interna destes ângulos , basta aplicar a fórmula

. Como o polígono é regular e, é constituido pelos vertices
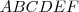
,ou seja é um hexagono , possui 6 lados .
Segue que ,
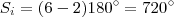
.
Não conseguir compreender sua solução , poderia explicar como chegou a esta conclusão
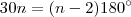
? comente qualquer coisa .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por sauloandrade » Dom Dez 30, 2012 14:44
por sauloandrade » Dom Dez 30, 2012 14:44
Olá santhiago.
O polígono não é um hexágono, pois pelo enunciado, ele é formado pelos vértices ABCDEF... Há uma reticência que significa que o polígono é formado por n vértices, e eu preciso determinar o valor de n para obter a soma dos ângulos internos.
Sobre minha resolução deixa eu explicar com exemplos:
Como eu disse, se eu pegar a soma dos ângulos internos de um polígono REGULAR e dividir por n eu terei o valor de cada ângulo interno. Pegue por exemplo, o quadrado. Sabemos que a soma dos ângulos internos é 360°e possui 4 lados. Dividindo a soma dos ângulos internos (360°) pelo número de lados (4), eu obterei o valor de cada ângulo interno do polígono, no caso 4 ângulos de 90°.
Então aplicando o mesmo raciocínio, teremos:

resolvendo n=2,4.
Isso não é possível, pois não existe polígono com número de lado 2,4. rs.
é ficou confuso por que eu não sei por fração no latex ai eu adiantei um pouco o cálculo, desculpa.
-
sauloandrade
- Usuário Ativo

-
- Mensagens: 23
- Registrado em: Dom Out 28, 2012 12:03
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por e8group » Dom Dez 30, 2012 16:14
por e8group » Dom Dez 30, 2012 16:14
Ok compreendo .
Nosso objetivo é obter o número de lados ,para calcular a soma interna dos ângulo .
Obs.: Tome cuidado , o ângulo
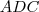
ser igual a
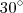
não implica que cada ângulo interno é igual
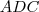
.
Observe a figura .
Vamos supor que cada ângulo interno meça

.
Pela nossa hipótese ,

.
Veja a figura como ilustração . Estou supondo que

,mas não necessariamente é verdade .
No triângulo

. Temos

.
No triângulo
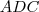
.Temos
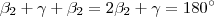
.
Mas para cada triângulo ,

.Temos que ,



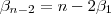
Assim ,
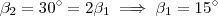
.
Lembrando que ,

implica

.
Conclusão ,
Temos por um lado que ,

. Entretanto por outro lado ,
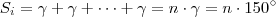
(n-vezes)
logo ,

.
Resolvendo encontrará

.
Portanto ,

.
Espero que estar certo . Comente qualquer coisa , tem gabarito ? .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por sauloandrade » Dom Dez 30, 2012 17:34
por sauloandrade » Dom Dez 30, 2012 17:34
Ahhh obrigado santhiago. Meu erro foi pensar que 30° seria um ângulo interno, o que não é verdade.
Sua resposta bate com o gabarito sim, obrigado

-
sauloandrade
- Usuário Ativo

-
- Mensagens: 23
- Registrado em: Dom Out 28, 2012 12:03
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por e8group » Dom Dez 30, 2012 17:51
por e8group » Dom Dez 30, 2012 17:51
Quando deparar com exercícios como este é importante fazer o desenho . Se permanecer dúvida só postar algo .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Ângulos internos do trapézio]
 por Gustavo Gomes » Qua Dez 19, 2012 22:37
por Gustavo Gomes » Qua Dez 19, 2012 22:37
- 1 Respostas
- 1428 Exibições
- Última mensagem por timoteo

Qui Dez 20, 2012 00:47
Geometria Plana
-
- [Trigonometria]Ângulos Internos
 por ALPC » Seg Jul 01, 2013 14:33
por ALPC » Seg Jul 01, 2013 14:33
- 2 Respostas
- 2270 Exibições
- Última mensagem por ALPC

Seg Jul 01, 2013 15:33
Trigonometria
-
- Angulos internos de um triangulo.
por albtec01 » Sáb Abr 12, 2014 19:19
- 0 Respostas
- 1033 Exibições
- Última mensagem por albtec01

Sáb Abr 12, 2014 19:19
Trigonometria
-
- furg- os números que expressam angulos internos
por Natalie » Sex Set 16, 2011 18:30
- 1 Respostas
- 1692 Exibições
- Última mensagem por MarceloFantini

Sex Set 16, 2011 18:45
Progressões
-
- Calculo dos angulos internos dum triangulo hiperbólico
por Jhenrique » Ter Jul 24, 2012 18:42
- 0 Respostas
- 1811 Exibições
- Última mensagem por Jhenrique

Ter Jul 24, 2012 18:42
Geometria Espacial
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
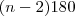 . Sabemos ainda que o polígono é regular então, se eu pegar a soma dos ângulos internos e dividir pelo número de lados eu obterei a medida de cada ângulo interno.
. Sabemos ainda que o polígono é regular então, se eu pegar a soma dos ângulos internos e dividir pelo número de lados eu obterei a medida de cada ângulo interno. resolvendo teremos
resolvendo teremos 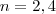 .
.

 . Como o polígono é regular e, é constituido pelos vertices
. Como o polígono é regular e, é constituido pelos vertices 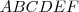 ,ou seja é um hexagono , possui 6 lados .
,ou seja é um hexagono , possui 6 lados . 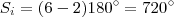 .
. 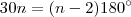 ? comente qualquer coisa .
? comente qualquer coisa .

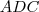 ser igual a
ser igual a 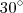 não implica que cada ângulo interno é igual
não implica que cada ângulo interno é igual  .
.  .
.  ,mas não necessariamente é verdade .
,mas não necessariamente é verdade . . Temos
. Temos  .
. 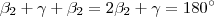 .
.  .Temos que ,
.Temos que , 


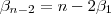
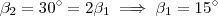 .
.  implica
implica  .
. 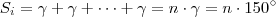 (n-vezes)
(n-vezes)  .
.  .
.  .
. 


 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.