Olá santhiago.
O polígono não é um hexágono, pois pelo enunciado, ele é formado pelos vértices ABCDEF... Há uma reticência que significa que o polígono é formado por n vértices, e eu preciso determinar o valor de n para obter a soma dos ângulos internos.
Sobre minha resolução deixa eu explicar com exemplos:
Como eu disse, se eu pegar a soma dos ângulos internos de um polígono REGULAR e dividir por n eu terei o valor de cada ângulo interno. Pegue por exemplo, o quadrado. Sabemos que a soma dos ângulos internos é 360°e possui 4 lados. Dividindo a soma dos ângulos internos (360°) pelo número de lados (4), eu obterei o valor de cada ângulo interno do polígono, no caso 4 ângulos de 90°.
Então aplicando o mesmo raciocínio, teremos:

resolvendo n=2,4.
Isso não é possível, pois não existe polígono com número de lado 2,4. rs.
é ficou confuso por que eu não sei por fração no latex ai eu adiantei um pouco o cálculo, desculpa.
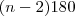 . Sabemos ainda que o polígono é regular então, se eu pegar a soma dos ângulos internos e dividir pelo número de lados eu obterei a medida de cada ângulo interno.
. Sabemos ainda que o polígono é regular então, se eu pegar a soma dos ângulos internos e dividir pelo número de lados eu obterei a medida de cada ângulo interno. resolvendo teremos
resolvendo teremos 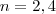 .
.

 . Como o polígono é regular e, é constituido pelos vertices
. Como o polígono é regular e, é constituido pelos vertices 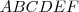 ,ou seja é um hexagono , possui 6 lados .
,ou seja é um hexagono , possui 6 lados . 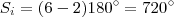 .
. 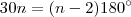 ? comente qualquer coisa .
? comente qualquer coisa .

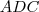 ser igual a
ser igual a 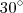 não implica que cada ângulo interno é igual
não implica que cada ângulo interno é igual  .
.  .
.  ,mas não necessariamente é verdade .
,mas não necessariamente é verdade . . Temos
. Temos  .
. 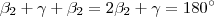 .
.  .Temos que ,
.Temos que , 


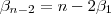
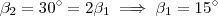 .
.  implica
implica  .
. 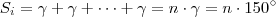 (n-vezes)
(n-vezes)  .
.  .
.  .
. 

 .
.



