 por manuel_pato1 » Sex Dez 07, 2012 20:08
por manuel_pato1 » Sex Dez 07, 2012 20:08
I =

Chamei de u = sin(x)/ cos(x) , logo, du/dx = 1/ cos²(x)
Daí eu meio que empaquei, pois não consigo fazer alguma relação trigonométrica com o '' 1 + x²'' do denominador
Alguém pode me ajudar? Abração
-
manuel_pato1
- Usuário Dedicado

-
- Mensagens: 33
- Registrado em: Ter Set 18, 2012 22:18
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
 por young_jedi » Sáb Dez 08, 2012 12:16
por young_jedi » Sáb Dez 08, 2012 12:16
só uma duvida a exponecial é realmente de tangente ou de
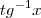
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por Russman » Sáb Dez 08, 2012 13:36
por Russman » Sáb Dez 08, 2012 13:36
Se fosse
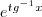
sairia muito mais fácil essa integral!
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por manuel_pato1 » Sáb Dez 08, 2012 13:56
por manuel_pato1 » Sáb Dez 08, 2012 13:56
Desculpem, o correto é:

também achei estranho, essa integral faz parte de uma lista que meu professor passou, mas acho que está errada.
Pois é, se fosse elevado na -1, daria pra fazer mais tranquilamente.
a respota é:

-
manuel_pato1
- Usuário Dedicado

-
- Mensagens: 33
- Registrado em: Ter Set 18, 2012 22:18
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
 por manuel_pato1 » Sáb Dez 08, 2012 13:58
por manuel_pato1 » Sáb Dez 08, 2012 13:58
acho que esse atg(x) ele quis dizer arctg(x)
-
manuel_pato1
- Usuário Dedicado

-
- Mensagens: 33
- Registrado em: Ter Set 18, 2012 22:18
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
 por Russman » Sáb Dez 08, 2012 14:04
por Russman » Sáb Dez 08, 2012 14:04
Então, perfeito. Só pra esclarecer

, ok?.
Agora, faça
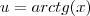
. Assim,

. Portanto

Agora integre trivialmente em

e faça a substituição contrária para expressar o resultado em termos de

.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por manuel_pato1 » Sáb Dez 08, 2012 15:02
por manuel_pato1 » Sáb Dez 08, 2012 15:02
Muito obrigado, Russman.
Consegui resolver, e bateu com o resultado.
Tô começando a matéria agora, então estou com umas dúvidas nessas integrais um pouco mais complicadinhas.
Abraço.
-
manuel_pato1
- Usuário Dedicado

-
- Mensagens: 33
- Registrado em: Ter Set 18, 2012 22:18
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- integral de função exponencial
por vivima » Sex Mai 09, 2014 13:36
- 2 Respostas
- 2005 Exibições
- Última mensagem por vivima

Sex Mai 09, 2014 15:19
Cálculo: Limites, Derivadas e Integrais
-
- [Função exponencial] Exercício sobre função exponencial
por fff » Ter Jan 07, 2014 17:51
- 3 Respostas
- 4067 Exibições
- Última mensagem por fff

Qua Jan 08, 2014 06:47
Funções
-
- Integral com exponencial
por suziquim » Ter Mai 10, 2011 18:07
- 2 Respostas
- 3216 Exibições
- Última mensagem por suziquim

Qua Mai 11, 2011 11:08
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Exponencial
por raulalves_ » Qua Abr 18, 2012 01:49
- 1 Respostas
- 1655 Exibições
- Última mensagem por LuizAquino

Qui Abr 19, 2012 14:59
Cálculo: Limites, Derivadas e Integrais
-
- [Desigualdade] entre função exponencial e função potência
por VitorFN » Sex Mai 26, 2017 15:18
- 1 Respostas
- 5738 Exibições
- Última mensagem por adauto martins

Sex Jul 07, 2017 12:17
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Balanar - Seg Ago 09, 2010 04:01
Simplifique a expressão com radicais duplos abaixo:
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
Resposta:
Dica:
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
(dica : igualar a expressão a

e elevar ao quadrado os dois lados)
Assunto:
Simplifique a expressão com radicais duplos
Autor:
MarceloFantini - Qua Ago 11, 2010 05:46
É só fazer a dica.
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Soprano - Sex Mar 04, 2016 09:49
Olá,
O resultado é igual a 1, certo?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




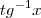

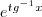 sairia muito mais fácil essa integral!
sairia muito mais fácil essa integral!




 , ok?.
, ok?.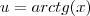 . Assim,
. Assim,  . Portanto
. Portanto
 e faça a substituição contrária para expressar o resultado em termos de
e faça a substituição contrária para expressar o resultado em termos de  .
.

![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)