Verifique se a função satisfaz as três hipoteses do Teorema de Rolle sobre o intervalo dado. Então encontre todos os numeros c que satisfazem a conclusao do teorema.
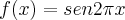 no intervalo [-1,1]
no intervalo [-1,1]Segundo a resolução do livro, a função é continua, ou seja, f(-1)=f(1), porém fazendo f(-1) não ficaria:
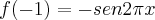 ? e travei na tentativa de resolver o f '(c), que seria:
? e travei na tentativa de resolver o f '(c), que seria: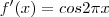 portanto pra calcular o c :
portanto pra calcular o c : 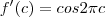 ---
--- 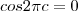 , não sei como sair daí! A resposta do problema é :
, não sei como sair daí! A resposta do problema é : 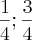
obrigada.


 é contínua em
é contínua em ![[a,b] [a,b]](/latexrender/pictures/2c3d331bc98b44e71cb2aae9edadca7e.png) e diferenciável em
e diferenciável em  . Supondo que
. Supondo que  teremos um
teremos um 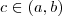 tal que
tal que 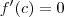 .
. ![[-1,1] [-1,1]](/latexrender/pictures/d060b17b29e0dae91a1cac23ea62281a.png) e
e 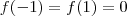 . Deste modo temos que , existe um
. Deste modo temos que , existe um  tal que
tal que 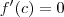 .
. 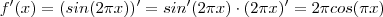 . Daí ,
. Daí , 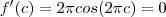 .Visto que ,
.Visto que , 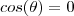 se
se 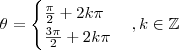 . Temos que ,
. Temos que , 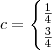 . (Verifique ! )
. (Verifique ! )
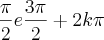
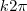 , onde
, onde  é o número inteiro que representa o número de voltas.
é o número inteiro que representa o número de voltas. e
e 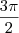 .
.


 .
.



