(UNIV. BLUMENAU) Ciclo Trigonométrico

[CarlosC]

Quando o relógio marca 3 horas, o menor ângulo formado pelos ponteiros mede 90º. Qual será o valor do ângulo maior formado pelos ponteiros quando o relógio marcar 12 horas e 15 minutos?

a) 90º
b) 87º
c) 270º
d) 277,5º
e) 272º 30'

Lá vai minha resolução: (Desculpe pela precariedade da imagem uhsahuas.. mas n consegui desenhar e peguei esse relogio e editei)



Como ele disse que quando marca 3 horas o ângulo que se forma é 90º, então cada hora é 30º

Calculando o angulo azul que eu chamei de z

60 min -------- 30º
15 min -------- z .:. z = 7º30'

Bem do ponteiro 12 ao 15 temos 3 horas, que vai ser o total (chamei de t)

60 min -------- 30º
180 min ------- T .:. T = 90º

Para achar o angulo vermelho (verde + azul = total)

z + v = T
7º30' + v = 90º .:. v = 82º30'

Sendo que essa opção nem tem no no gabarito.

E o gabarito >> D) 277,5º

Alguém poderia explicar oq eu fiz errado ? :\

Obrigado :]

[Molina]

Seja bem-vindo, Carlos.

Note que o ângulo vermelho (que por sinal eu não vi no desenho, mas suponho que seja o maior ângulo formado pelos ponteiros) é na verdade:

360°- (ângulo verde)

= 360° - 82°30'

= 360° - 82,5°

= 277,5°


Conseguiu ver isso agora?

[CarlosC]

Consegui sim.

Com relação ao desenho eu esqueci do angulo mesmo, porém foi oq vc comentou ("o maior ângulo formado pelos ponteiros") .

Muito Obrigado!

Abraços

[Molina]

É isso mesmo Carlos.

Aí vai uma dica de como calcular o menor ângulo formado pelos ponteiros do relógio:



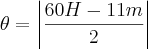
Com essa fórmula não tem erro. Basta substituir o H pelo valor correspondente as horas e o m pelo valor correspondente ao minutos. Lembrando que você sempre descobre o menor ângulo formado pelos ponteiros.

Verifique esta fórmula no seu exemplo, não esquecendo de considerar a hora como sendo 0 e os minutos como sendo 15. Considere as horas como sendo zero pois 12:15 = 00:15pm.

O valor que você vai encontrar vai ser o menor valor.
Logo faça 360° menos este valor.

Depois comente caso tenha dado certo e verifique para outros valores.

[CarlosC]

Fantástica a dica, funcionou com esse exemplo pelo menos.

Amanhã de manhã irei testar com os que eu fiz hoje pq agora já guardei tudo.

Mais uma vez muito obrigado pela resolução e pela dica! ;D

Vlw!