![\sqrt[]{{x}^{2}-1}](/latexrender/pictures/c3237320b22a2fbc333cdf2dd6e37f33.png "\sqrt[]{{x}^{2}-1}")
. dê a resposta em termos de intervalos.![{x}^{2}-1>0 \Rightarrow {x}^{2}>1 \Rightarrow x > \sqrt[]{1}](/latexrender/pictures/a133e567e7062fdb941f1f8646bb1b87.png "{x}^{2}-1>0 \Rightarrow {x}^{2}>1 \Rightarrow x > \sqrt[]{1}")
D= {x e R/ x>
![\sqrt[]{1}](/latexrender/pictures/c27c91cace800eaf0a3cd0936a90638a.png "\sqrt[]{1}")
}
por jose henrique » Ter Out 26, 2010 23:37
. dê a resposta em termos de intervalos.}
por MarceloFantini » Qua Out 27, 2010 04:32
. Assim,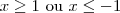 
. Geometricamente, é uma parábola de boca para cima, e ela é positiva nos valores antes de -1 e depois de 1, e zerando nesses pontos.
por jose henrique » Qua Out 27, 2010 20:23
por MarceloFantini » Qua Out 27, 2010 20:43
? Isso está dentro da raíz quadrada, eu apenas trabalhei com a restrição. A passagem 
usa esse fato: 
. Lembre-se, também, que módulo quer dizer distância até a origem. Quando dizemos que 
, queremos o conjunto de todos os pontos cuja distância até a origem é menor do que 3. Da mesma maneira, 
quer dizer todos os pontos cuja distância até a origem é maior ou igual a um. Isso tem duas respostas: os pontos maiores ou iguais a um OU os pontos menores ou iguais a menos um, afinal de contas, a distãncia de um até a origem é a mesma distância de -1 até a origem.Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
