Usar coordenadas cilíndricas ou esféricas para calcular a expressão:
![\int_{0}^{a}\int_{0}^{\sqrt[2]{a^2-x^2}}\int_{0}^{\sqrt[2]{a^2-x^2-y^2}}x^2 dz dy dx \int_{0}^{a}\int_{0}^{\sqrt[2]{a^2-x^2}}\int_{0}^{\sqrt[2]{a^2-x^2-y^2}}x^2 dz dy dx](/latexrender/pictures/0b8d4c3cb95f41b672f0bb945d260fb5.png)
Sei que a superfície superior do sólido vai ser
 e passando isso para coordenadas cilíndricas, eu fico com
e passando isso para coordenadas cilíndricas, eu fico com 
A superfície inferior vai ser um plano xy de equação z = 0
e pelos limites de integração em x e y, a projeção R é a região do plano xy delimitada pelo círculo
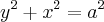
então o ângulo
 vai variar de 0 a
vai variar de 0 a 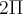
r vai variar de 0 a a
e o integrando que é x² eu vou ter que mudar para

ficando assim:
![\int_{0}^{2\Pi}\int_{0}^{a}\int_{0}^{a^2-r^2}[r^2 - (rsen\Theta)^2]dz dr d\Theta \int_{0}^{2\Pi}\int_{0}^{a}\int_{0}^{a^2-r^2}[r^2 - (rsen\Theta)^2]dz dr d\Theta](/latexrender/pictures/490f925865996e77feeb57cf71a59e44.png)
mas a resolução está ficando muito extensa e complicada, então não sei se está certo.
O que vocês acham? Eu estou fazendo errado? Tem outra maneira de fazer isso que seja mais simples?


 em torno de uma esfera de raio a. O Jacobiano para esta situação(coordenadas esféricas) é:
em torno de uma esfera de raio a. O Jacobiano para esta situação(coordenadas esféricas) é: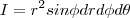 com
com 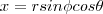
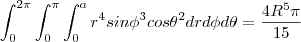
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
