está fazendo desaparecer o Mar de Aral, na Ásia, que,
segundo especialistas, estará totalmente seco em 2010.
... Nas últimas quatro décadas, perdeu 60% de sua superfície
e 3/4 do volume de água.
1) Admita que o volume V de água, nesse período, tenha diminuído, a uma taxa anual constante, de
acordo com a função:
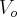volume há 40 anos i taxa centesimal anual de diminuição do volume
t tempo medido em anos
tentei resolver assim:
![\frac{3}{4}=1*{\left(1-i \right)}^{40} \Rightarrow \sqrt[40]{\frac{3}{4}}=1-i \Rightarrow 1-\sqrt[40]{\frac{3}{4}}= i](/latexrender/pictures/260af2112953805e5b8eb9566e8e8a1c.png "\frac{3}{4}=1*{\left(1-i \right)}^{40} \Rightarrow \sqrt[40]{\frac{3}{4}}=1-i \Rightarrow 1-\sqrt[40]{\frac{3}{4}}= i")
desde já agredeço a atençao!!!
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}")
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}")
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png "{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}")
da seguinte forma:
.
da seguinte forma:
.