 por Balanar » Sex Out 15, 2010 21:15
por Balanar » Sex Out 15, 2010 21:15
Na figura, temos:

Determine:
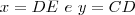

Resposta:
 Resolução:
Resolução: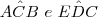
possuem lados respectivamente perpendiculares.
Daí:


Logo:

Então:
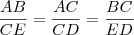
Logo:
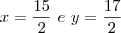
Minha dúvida é a seguinte :
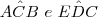
possuem lados respectivamente perpendiculares.
Daí:

Não to prosseguindo ver essa parte.
-
Balanar
- Usuário Parceiro

-
- Mensagens: 72
- Registrado em: Qua Dez 03, 2008 07:18
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Perimetro de 2 triangulos semelhantes
 por aldss » Seg Out 26, 2015 23:34
por aldss » Seg Out 26, 2015 23:34
- 0 Respostas
- 905 Exibições
- Última mensagem por aldss

Seg Out 26, 2015 23:34
Trigonometria
-
- [Geometria Plana - Triângulo] Triângulo Isós. e Bissetriz
por raimundoocjr » Qua Fev 22, 2012 09:41
- 3 Respostas
- 6601 Exibições
- Última mensagem por DanielFerreira

Sáb Fev 25, 2012 01:37
Geometria Plana
-
- Triangulo
por ginrj » Ter Abr 28, 2009 20:58
- 3 Respostas
- 3785 Exibições
- Última mensagem por ginrj

Sáb Mai 02, 2009 12:30
Geometria Plana
-
- Triângulo.
por Molina » Qua Mai 13, 2009 23:20
- 2 Respostas
- 2147 Exibições
- Última mensagem por Molina

Qui Mai 14, 2009 19:04
Geometria Plana
-
- Triângulo
por cristina » Seg Set 14, 2009 18:49
- 5 Respostas
- 3023 Exibições
- Última mensagem por Marcampucio

Ter Set 15, 2009 16:44
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

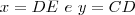


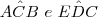 possuem lados respectivamente perpendiculares.
possuem lados respectivamente perpendiculares.


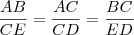
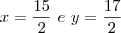
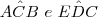 possuem lados respectivamente perpendiculares.
possuem lados respectivamente perpendiculares.


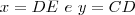


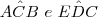 possuem lados respectivamente perpendiculares.
possuem lados respectivamente perpendiculares.


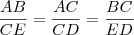
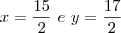
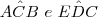 possuem lados respectivamente perpendiculares.
possuem lados respectivamente perpendiculares.

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.