Há 12 moças e 10 rapazes, onde 5 deles (3 moças e 2 rapazes) são irmão e os restantes não possuem parentesco. Quantos são os casamentos possíveis?
* Para a letra a, sei que devemos separar os subconjuntos de um elemento, dois elementos, três elementos, e quatro elementos.Então, fiz o seguinte:
-> Há
 subconjuntos de um elemento;
subconjuntos de um elemento;-> Há
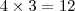 subconjuntos de dois elementos;
subconjuntos de dois elementos;-> Há
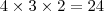 subconjuntos de dois elementos;
subconjuntos de dois elementos;-> Há
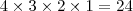 subconjuntos de dois elementos.
subconjuntos de dois elementos.Assim, há
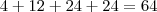 subconjuntos do conjunto {a,b.c.d}.
subconjuntos do conjunto {a,b.c.d}.Mas a resposta correta que está no livro é 16; qual foi o meu erro?
Para a letra b eu gostaria de saber que tipo de calculo é utilizado.


