 por natanskt » Sex Out 08, 2010 20:05
por natanskt » Sex Out 08, 2010 20:05
(AFA) - a soma das raizes da equação
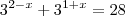
resolução
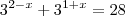



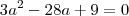
queria saber daonde veio esse

????
os outros eu sei mais tentei e não encontrei como chegar a essa equação
por favor quem souber me ajude aew a intender essa passagem da penultima pela ultima
-
natanskt
- Colaborador Voluntário

-
- Mensagens: 176
- Registrado em: Qua Out 06, 2010 14:56
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: nenhum
- Andamento: cursando
 por Molina » Sex Out 08, 2010 20:57
por Molina » Sex Out 08, 2010 20:57
natanskt escreveu:(AFA) - a soma das raizes da equação
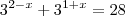
resolução
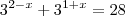



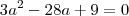
queria saber daonde veio esse

????
os outros eu sei mais tentei e não encontrei como chegar a essa equação
por favor quem souber me ajude aew a intender essa passagem da penultima pela ultima
Boa noite, Natan.
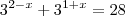


Chamando

e substituindo...
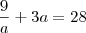
Acho que aqui é sua dúvida! Precisamos tirar o
mínimo múltiplo comum de tudo:
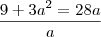
Como
a está dividindo toda igualdade podemos "cortar" ele...

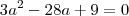
Agora usando Báskara você pode encontrar
a' e
a''. Substituir esses valores em

e achar os
x.
Caso não consiga informe.
(Caso consiga informe também)

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por natanskt » Sex Out 08, 2010 22:15
por natanskt » Sex Out 08, 2010 22:15
valeu !!!
eu conseguir!
graças a sua explicação detalhada
muito obrigado!qualquer dia eu te pago uma cerveja ahsuhasuhu
-
natanskt
- Colaborador Voluntário

-
- Mensagens: 176
- Registrado em: Qua Out 06, 2010 14:56
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: nenhum
- Andamento: cursando
 por Molina » Sex Out 08, 2010 22:19
por Molina » Sex Out 08, 2010 22:19
natanskt escreveu:valeu !!!
eu conseguir!
graças a sua explicação detalhada
muito obrigado!qualquer dia eu te pago uma cerveja ahsuhasuhu
Não fala duas vezes que senão eu vou cobrar, hahaha!
Bom estudo!

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Equação Exponenciais
por umaiafilho » Qui Mai 12, 2011 21:35
- 2 Respostas
- 1270 Exibições
- Última mensagem por umaiafilho

Qui Mai 12, 2011 23:02
Sistemas de Equações
-
- Equação Exponenciais
por umaiafilho » Sex Mai 13, 2011 09:02
- 2 Respostas
- 1305 Exibições
- Última mensagem por umaiafilho

Sex Mai 13, 2011 09:24
Sistemas de Equações
-
- Equação Exponenciais
por umaiafilho » Sáb Mai 14, 2011 11:50
- 2 Respostas
- 1263 Exibições
- Última mensagem por umaiafilho

Sáb Mai 14, 2011 14:16
Sistemas de Equações
-
- Equação Exponenciais
por umaiafilho » Sáb Mai 14, 2011 17:12
- 4 Respostas
- 1957 Exibições
- Última mensagem por umaiafilho

Sáb Mai 14, 2011 20:09
Sistemas de Equações
-
- Exponenciais
por Souo » Ter Jun 30, 2015 01:42
- 3 Respostas
- 2695 Exibições
- Última mensagem por nakagumahissao

Sex Jul 03, 2015 21:24
Logaritmos
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
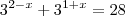
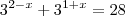



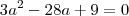
 ????
????
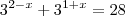
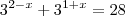



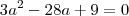
 ????
????
????
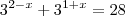


 e substituindo...
e substituindo...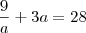
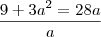

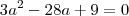
 e achar os x.
e achar os x.


