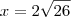por natanskt » Sex Out 08, 2010 12:37
por natanskt » Sex Out 08, 2010 12:37
o conjunto solução da equação
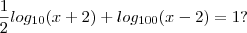
a-)
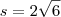
b-)a-)
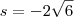
c-)
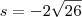
d-)a-)
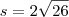
e-)a-)
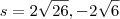
-
natanskt
- Colaborador Voluntário

-
- Mensagens: 176
- Registrado em: Qua Out 06, 2010 14:56
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: nenhum
- Andamento: cursando
 por natanskt » Sex Out 08, 2010 16:11
por natanskt » Sex Out 08, 2010 16:11
tenho muitos exercicios aqui,tenho uma apostila de um curso preparatorio a distancia,tenho exercicios de matematica,fisica etc...e provas tambem
estou estudando pra entrar na AFA,pega meu msn
natan3tskt@hotmail.comnois converssa lá
-
natanskt
- Colaborador Voluntário

-
- Mensagens: 176
- Registrado em: Qua Out 06, 2010 14:56
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: nenhum
- Andamento: cursando
 por DanielRJ » Sex Out 08, 2010 16:41
por DanielRJ » Sex Out 08, 2010 16:41
natanskt escreveu:tenho muitos exercicios aqui,tenho uma apostila de um curso preparatorio a distancia,tenho exercicios de matematica,fisica etc...e provas tambem
estou estudando pra entrar na AFA,pega meu msn
natan3tskt@hotmail.comnois converssa lá
Já add.. mas o meu objetivo é somente matematica eu to muito ruim...
-

DanielRJ
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Sex Ago 20, 2010 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- (AMAN) Equação logaritmica
por natanskt » Seg Out 11, 2010 16:20
- 2 Respostas
- 1385 Exibições
- Última mensagem por natanskt

Seg Out 11, 2010 17:13
Logaritmos
-
- (AMAN) inequação logaritmica
por natanskt » Sex Out 29, 2010 10:19
- 0 Respostas
- 910 Exibições
- Última mensagem por natanskt

Sex Out 29, 2010 10:19
Logaritmos
-
- (AMAN) função logaritmica
por natanskt » Sex Out 29, 2010 10:27
- 1 Respostas
- 1534 Exibições
- Última mensagem por DanielFerreira

Qui Nov 18, 2010 17:46
Logaritmos
-
- (ITA) equaçoes logaritmica
por natanskt » Seg Out 11, 2010 17:11
- 6 Respostas
- 4638 Exibições
- Última mensagem por Elcioschin

Qua Out 13, 2010 22:55
Logaritmos
-
- (ITA) equaçoes logaritmica
por natanskt » Qua Out 13, 2010 18:16
- 2 Respostas
- 1360 Exibições
- Última mensagem por MarceloFantini

Sex Out 15, 2010 17:25
Logaritmos
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
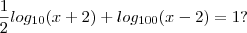
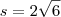
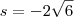
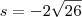
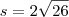
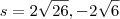

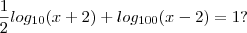
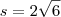
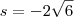
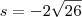
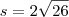
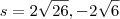

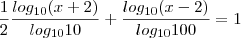
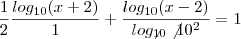
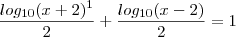
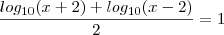
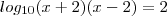

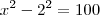
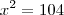
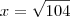
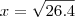
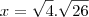
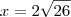
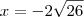
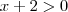 porque é o logaritmano e
porque é o logaritmano e 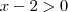 idem.
idem. ---> Ok! e
---> Ok! e  ---Ok!
---Ok!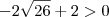 ---> Falso e
---> Falso e 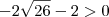 -----> Falso
-----> Falso