 por DanielRJ » Qua Out 06, 2010 17:20
por DanielRJ » Qua Out 06, 2010 17:20
São dados log 2= 0,30 e log 3 = 0,48 . O numero Real x, que é solução da equação
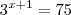
é tal que:
a)x<=0
b)0<x<=2
c)2<x<=3
d)3<x<=5
e)x>5
Bom eu fiz a conta de 2 jeitos vou demonstrar a mais fácil para um melhor entendimento.
(log^25 = log de 25 na base 3 idem os outros.)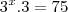
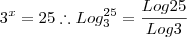
por fim achei
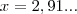
Minha pergunta é no primeiro modo que eu fiz

por sinal uma volta imensa que nem da pra demonstrar os calculo obtive x=5/6 queria saber qual dos dois resultados está correto e onde eu encaixo eles na resposta desde já Obrigado!!!
-

DanielRJ
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Sex Ago 20, 2010 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por MarceloFantini » Qua Out 06, 2010 17:58
por MarceloFantini » Qua Out 06, 2010 17:58
Os dois estão corretos, a diferença é a quantidade de cálculos necessária.
Primeiro método:
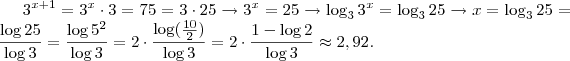
Segundo método:
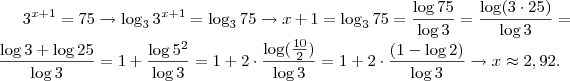
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Logaritmos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Logaritmos] Dúvida em um exercicio envolvendo logaritmos.
por LuizGustavo » Sex Jun 01, 2012 22:48
- 2 Respostas
- 5042 Exibições
- Última mensagem por jefferson0209

Ter Set 22, 2015 18:38
Logaritmos
-
- [Logaritmos] equação com logaritmos
por natanaelvoss » Sex Dez 07, 2012 20:25
- 2 Respostas
- 6670 Exibições
- Última mensagem por jefferson0209

Ter Set 22, 2015 18:40
Logaritmos
-
- logaritmos
por celisecorrea » Ter Set 30, 2008 17:17
- 2 Respostas
- 3362 Exibições
- Última mensagem por jefferson0209

Ter Set 22, 2015 18:38
Logaritmos
-
- LOGARITMOS
por DESESPERADA » Qua Dez 30, 2009 13:25
- 2 Respostas
- 3132 Exibições
- Última mensagem por jefferson0209

Ter Set 22, 2015 18:37
Matemática Financeira
-
- Logaritmos
por cristina » Qua Jun 02, 2010 10:07
- 1 Respostas
- 2422 Exibições
- Última mensagem por Cleyson007

Qua Jun 02, 2010 13:30
Logaritmos
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
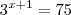 é tal que:
é tal que: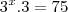
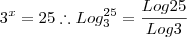
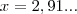
 por sinal uma volta imensa que nem da pra demonstrar os calculo obtive x=5/6 queria saber qual dos dois resultados está correto e onde eu encaixo eles na resposta desde já Obrigado!!!
por sinal uma volta imensa que nem da pra demonstrar os calculo obtive x=5/6 queria saber qual dos dois resultados está correto e onde eu encaixo eles na resposta desde já Obrigado!!!

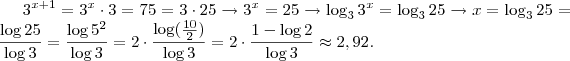
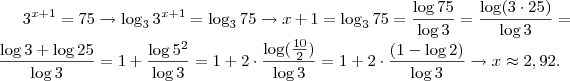



 .
.



