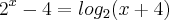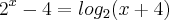por Kirie » Ter Out 05, 2010 23:08
por Kirie » Ter Out 05, 2010 23:08
Fantini, essa equação é original, foi retirada do Livro do Cursinho Objetivo,Vestibular MACKENZIE não relacionando o ano, segue o Enunciado:
(MACK) As soluções reais da Equação (............) estão nos intervalos:
a){-4,-3} e {1,2}
b){-3,-2} e {2,3}
c){-4,-3} e {3,4}
d){-4,-3} e {2,3}
e){-2,-1} e {1,2}
Também não encontrei um método para resolução, exceto o gráfico. Se encontrar por favor me avise ! um abraço e agradeço pela atenção !