 por sukita » Ter Out 05, 2010 22:22
por sukita » Ter Out 05, 2010 22:22
ola estou estudando para um concurso com uma apostila q eh uma lastima... e td mal explicado, o resultado eh mto simplificado e a parte teorica mto escassa, sendo assim tenho duvidas nessas questoes.. calcule f

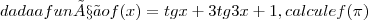
desde jah obg
-
sukita
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Qui Set 09, 2010 19:31
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Técnico em química
- Andamento: formado
Voltar para Progressões
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Dúvidas
 por Adriana Barbosa » Seg Jun 01, 2009 11:01
por Adriana Barbosa » Seg Jun 01, 2009 11:01
- 1 Respostas
- 1711 Exibições
- Última mensagem por Molina

Ter Jun 02, 2009 07:00
Funções
-
- Duvidas
 por Paulo A G » Qua Jan 26, 2011 14:45
por Paulo A G » Qua Jan 26, 2011 14:45
- 1 Respostas
- 2994 Exibições
- Última mensagem por Molina

Qua Jan 26, 2011 15:09
Pedidos de Materiais
-
- 2 dúvidas
por analuiza » Qui Fev 17, 2011 23:14
- 1 Respostas
- 2714 Exibições
- Última mensagem por Molina

Sex Fev 18, 2011 13:33
Trigonometria
-
- Dúvidas ....
por vanessa134 » Seg Out 17, 2011 01:06
- 0 Respostas
- 1503 Exibições
- Última mensagem por vanessa134

Seg Out 17, 2011 01:06
Álgebra Elementar
-
- Dúvidas D:
por Aliiine » Seg Out 24, 2011 11:12
- 1 Respostas
- 2017 Exibições
- Última mensagem por jose henrique

Seg Out 24, 2011 22:47
Estatística
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

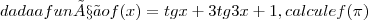


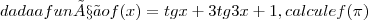

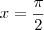 . Veja:
. Veja: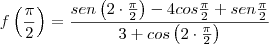

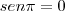
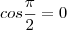
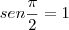





 .
.



