por mastercgmr » Ter Out 05, 2010 11:57
por mastercgmr » Ter Out 05, 2010 12:25
por MarceloFantini » Ter Out 05, 2010 17:00
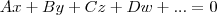, onde as letras maiores são constantes. Note que não há termos mistos (coisas como 
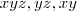). Logo, na primeira pergunta sobra a 2ª opção.
. Se 
e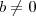 
, então ![z = \frac{b}{a}{/tex]. Se [tex]a=0](/latexrender/pictures/67d0aec7a1cb4ef5a3be183cb66fd570.png "z = \frac{b}{a}{/tex]. Se [tex]a=0")
e , 
não existe. Se 
e 
, tem infinitas soluções: 
.
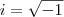. Um número complexo é da forma 
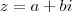, com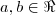 
.Dê uma estudada nesse assunto e tente novamente.
por mastercgmr » Ter Out 05, 2010 19:20
por DanielRJ » Ter Out 05, 2010 19:26
por mastercgmr » Ter Out 05, 2010 19:28
por mastercgmr » Qui Out 14, 2010 18:55
Na primeira pergunta não tive lá grande dificuldade, deu-me a 3ª opção. Na segunda pergunta não entendo o conceito de "dimensão de V" já traduzi o sistema para matriz e resolvi mas dai não sei mesmo o que fazer mais... Na terceira creio que a resposta é a segunda opção também não tenho muitas duvidas... Na quarta e na quinta não sei mesmo por onde pegar... não vou estar a tentar adivinhar... Na sexta, sei resolver um exercício de transformação linear mas não entendo o contexto do exercício 
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}")
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}")
zig escreveu:
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png "{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}")
da seguinte forma:
.
da seguinte forma:
.