Olá , boa noite , gostaria que me ajudassem com esse problema :
- Preciso dividir - > 15x³-6x²-35x+14 por 3x²-7
Obrigada !
por Luiza » Seg Out 04, 2010 19:24
por MarceloFantini » Seg Out 04, 2010 22:21
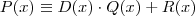
e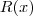 
. Note que se 
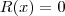, então 
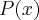é divisível por 
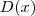e . Como resolver: procure montar um sistema como você aprendeu a fazer divisão de números, só que agora serão polinômios.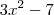 
na chave e 
fora. Agora vamos ver: um fator 
tal que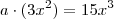 
. Dividindo por 
, com 
, encontramos que 
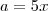. Só que, ao fazer isso, também multiplicamos 
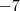por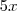 
. Isso significa que, do polinômio inicial, subtraímos 
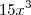e 
: 
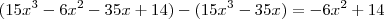. Sobrou o polinômio 
. 
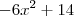tal que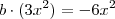 
, e esse fator é 
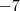. Multiplicando por e subtraindo o polinômio resultante: 
. Como o grau do divisor é maior que o grau do resto, a divisão pára e o resto 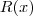é o que sobrou. Veja: 
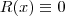, portanto o polinômio 
é divisível por 
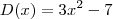e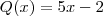 
. Escrevendo na forma do algoritmo da divisão: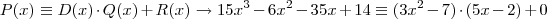
por Luiza » Seg Out 04, 2010 22:57
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}")
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}")
zig escreveu:
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png "{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}")
da seguinte forma:
.
da seguinte forma:
.