Preciso classifica-los, quanto ao número de soluções dizendo se são: Determinado, indeterminado, impossível, etc.
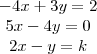
Obs.: Estou tentando pelo método de escalonamento de matriz, isso está correto ou é por outro método? Por favor, poderiam me ajudar?

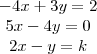


 e
e 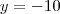 .
. .
.
 o sistema é impossível no conjunto
o sistema é impossível no conjunto  , para qualquer outro valor, o sistema é definido, admite apenas a solução
, para qualquer outro valor, o sistema é definido, admite apenas a solução 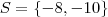 .
.
filipepaixao escreveu:não é possivel colocar numa matriz visto que não daria uma matriz quadrada

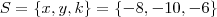 , e então conclui-se o problema.
, e então conclui-se o problema.


Voltar para Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.