 por jose henrique » Qui Set 30, 2010 21:35
por jose henrique » Qui Set 30, 2010 21:35
Numa pg estritamente decrescente, sabe-se que a1+a10=-513 e a4*a7=512. Determine a razão dessa Pg.
bem eu comecei a fazer assim:
se:
a4 * a7 = 512 então a5 * a6 = 512
aí eu peguei e fiz assim:
a5 * (a5 * q) = 512
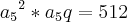
mas não consegui sair daí, o que fiz de errado?
-
jose henrique
- Colaborador Voluntário

-
- Mensagens: 129
- Registrado em: Qui Ago 12, 2010 20:32
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: outros
- Andamento: formado
 por DanielRJ » Sex Out 01, 2010 21:14
por DanielRJ » Sex Out 01, 2010 21:14
Vou dar um UP aqui porque quero que alguem responda até o momento só fiz questão desse tipo envovlvendo P.A
-

DanielRJ
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Sex Ago 20, 2010 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Loretto » Sáb Out 02, 2010 03:02
por Loretto » Sáb Out 02, 2010 03:02
Porque Fantini fez a1*a*10 = a4*a7 ?
Não deveria ser a4*a7 = a1*a4 = 512 ?
-
Loretto
- Usuário Dedicado

-
- Mensagens: 28
- Registrado em: Dom Jul 25, 2010 01:35
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: exatas
- Andamento: cursando
 por MarceloFantini » Sáb Out 02, 2010 11:55
por MarceloFantini » Sáb Out 02, 2010 11:55
Sim,
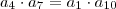
porque são equidistantes. Você mesmo usou esse fato ao tentar trabalhar com

.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por DanielRJ » Sáb Out 02, 2010 11:59
por DanielRJ » Sáb Out 02, 2010 11:59
Fantini escreveu:Sim,
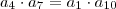
porque são equidistantes. Você mesmo usou esse fato ao tentar trabalhar com

.
Eu não foi o jose henrique mas eu poderia pegar o

e
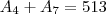
poderia fazer isso tambem?
-

DanielRJ
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Sex Ago 20, 2010 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por MarceloFantini » Sáb Out 02, 2010 12:24
por MarceloFantini » Sáb Out 02, 2010 12:24
Não, pois não é uma P.A., e mesmo na P.A. a soma de dois termos equidistantes é o dobro do termo médio.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Loretto » Sáb Out 02, 2010 18:14
por Loretto » Sáb Out 02, 2010 18:14
" Não, pois não é uma P.A., e mesmo na P.A. a soma de dois termos equidistantes é o dobro do termo médio. "
[tex] ak = (ak-1 + ak + 1)/2/tex]
na questão, a PG : a1,a2,a3,a4,a5,a6,a7,a8,a9,a10 , temos :
a1 = a10
a2 = a9
a3 = a8
a4 = a7
a5 = a6
Obrigado Pessoal !!
-
Loretto
- Usuário Dedicado

-
- Mensagens: 28
- Registrado em: Dom Jul 25, 2010 01:35
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: exatas
- Andamento: cursando
 por Loretto » Sáb Out 02, 2010 18:14
por Loretto » Sáb Out 02, 2010 18:14
" Não, pois não é uma P.A., e mesmo na P.A. a soma de dois termos equidistantes é o dobro do termo médio. "

na questão, a PG : a1,a2,a3,a4,a5,a6,a7,a8,a9,a10 , temos :
a1 = a10a2 = a9
a3 = a8
a4 = a7a5 = a6
Obrigado Pessoal !!
-
Loretto
- Usuário Dedicado

-
- Mensagens: 28
- Registrado em: Dom Jul 25, 2010 01:35
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: exatas
- Andamento: cursando
 por jose henrique » Ter Out 05, 2010 00:32
por jose henrique » Ter Out 05, 2010 00:32
fantini, quando vc falou:
"resolvendo, a1=- 1 ou a1 = -512"
eu não entendi como vc chegou a este resultado?
poderia explicar por favor?
desde já obrigado!
-
jose henrique
- Colaborador Voluntário

-
- Mensagens: 129
- Registrado em: Qui Ago 12, 2010 20:32
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: outros
- Andamento: formado
 por MarceloFantini » Ter Out 05, 2010 00:35
por MarceloFantini » Ter Out 05, 2010 00:35
É só resolver a equação do segundo grau na variável
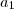
.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Progressões
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
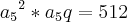

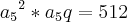




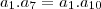

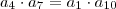 porque são equidistantes. Você mesmo usou esse fato ao tentar trabalhar com
porque são equidistantes. Você mesmo usou esse fato ao tentar trabalhar com  .
.

porque são equidistantes. Você mesmo usou esse fato ao tentar trabalhar com
.
 e
e 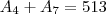 poderia fazer isso tambem?
poderia fazer isso tambem?








 .
.



