 por mavizinha » Qua Set 29, 2010 11:49
por mavizinha » Qua Set 29, 2010 11:49
Vocêsc me ajudaram muito no outro tópico, muito obrigada, mas na hora dos estudos travei de novo em outro problema
determine os valores do número a para os quais a função f não tem ponto crítico
f(x)=(a²+a-6)cos2x + (a-2)x + cos1
Agradeço desde já!!!!
-
mavizinha
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qua Set 15, 2010 22:38
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 7 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


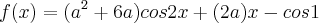




 .
.



