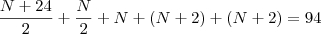A classificação destes desafios em fáceis, médios e difíceis, é apenas ilustrativa.
Eventualmente, o que pode ser difícil para a maioria, pode ser fácil para você e vice-versa.
Regras do fórum
A classificação destes desafios em fáceis, médios e difíceis, é apenas ilustrativa.
Eventualmente, o que pode ser difícil para a maioria, pode ser fácil para você e vice-versa.
 por ludmila » Sáb Jun 28, 2008 12:28
por ludmila » Sáb Jun 28, 2008 12:28
sao 8 garotas a passear....
Sheila é a mais velha da tturma e tem 12 anos a mais do que Geralda. Geralda tem a metade da idade de Nadia. Nadia é 2 anos mais nova do que Paula, que por sua vez tem a mesma idade de Priscilaa. Hortencia tem 8 anos, quase o dobro da idade de Olinda > Olinda tem 6 anos a mais do que Irene : levando-se em consideracao que a soma da idade de cada uma delas é igual a 104 , responda : qal a idade de cada uma delas?
por gentileza poderia me orientar a resolver este desafio???

-
ludmila
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Sáb Jun 28, 2008 12:04
- Formação Escolar: GRADUAÇÃO
- Área/Curso: biologicas
- Andamento: cursando
 por Molina » Sáb Jun 28, 2008 19:10
por Molina » Sáb Jun 28, 2008 19:10
Bom, nao tenho nenhuma certeza se essa é a resposta, porém, a soma das idades deu 104, respeitando todas informações (só a da "dobro da idade" que ficou meio confusa) do enunciado.
A forma que eu fiz foi a seguinte:
Irene = 0 anos
Olina = Irene + 6 = 6 anos
Hortência = 8 anos
Total 14 anos.
Temos 90 anos entao para distribuir pras outras 5 garotas:
Priscila = Paula
Nádia = Paula - 2
Geralda = Nádia/2
Sheila = Geralda + 12
dessas condições:
Priscila: 20,5 anos
Paula: 20,5 anos
Nádia: 18,5 anos
Geralda: 9,25 anos
Sheila: 21,25 anos
Total: 90 anos
90 anos + 14 anos = 104 anos.
É isso.
Vou esquematizar melhor minha equação quando der tempo.
Boa gincana!

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por DanielFerreira » Dom Jul 26, 2009 12:00
por DanielFerreira » Dom Jul 26, 2009 12:00
Esse problema está mal formulado!
S = G + 2

P = N + 2
P = Pr
H = 8H = 2 * O ==> 8 = 2O ==>
O = 4O = 6 + I ==> 4 = I + 6 ==>
I = - 2Isolando as expressões...
P = Pr = N + 2G = N/2S = G + 12 ==> S = N/2 + 12 ==>
S = (N + 24)/2S + G + N + P + Pr + H + O + I = 104
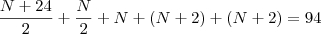
N + 12 + 3N + 4 = 94
4N = 78
N = 19,5S = 21,75
S = 21 anos e 9 mesesG = 9,75
G = 9 anos e 9 mesesP = Pr = 21,5Respota em
azul"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Desafios Fáceis
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Idades
por admin » Sáb Jul 21, 2007 01:20
- 3 Respostas
- 4656 Exibições
- Última mensagem por admin

Dom Nov 18, 2007 01:27
Desafios Difíceis
-
- Idades
por Jeffson » Qua Fev 04, 2009 23:53
- 1 Respostas
- 1791 Exibições
- Última mensagem por Neperiano

Seg Fev 09, 2009 11:09
Desafios Médios
-
- idades
por matematica86457m » Ter Jun 24, 2014 16:24
- 0 Respostas
- 1189 Exibições
- Última mensagem por matematica86457m

Ter Jun 24, 2014 16:24
Aritmética
-
- idades
por matematica86457m » Ter Jun 24, 2014 19:25
- 0 Respostas
- 1149 Exibições
- Última mensagem por matematica86457m

Ter Jun 24, 2014 19:25
Aritmética
-
- Outro de idades
por admin » Sáb Jul 21, 2007 01:13
- 2 Respostas
- 2141 Exibições
- Última mensagem por Neperiano

Ter Jun 16, 2009 17:18
Desafios Médios
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.