 por andrelpti » Dom Set 05, 2010 21:39
por andrelpti » Dom Set 05, 2010 21:39
Pessoal boa noite !!
Poderiam me ajudar com este calculo simplificar, não estou conseguindo fazer.
(2^? . 5^3)^-3 . (2 . 5^?)^3
Obrigado
-
andrelpti
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Dom Set 05, 2010 14:21
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Redes
- Andamento: cursando
 por andrelpti » Seg Set 06, 2010 17:49
por andrelpti » Seg Set 06, 2010 17:49
Dan,
Não lembrava que teria que tirar o mmc do 5^-9 . 5^9/5.
Muito obrigado !!!!
-
andrelpti
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Dom Set 05, 2010 14:21
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Redes
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Potência de raiz de raiz com subtração
 por Sergio filho » Sáb Dez 05, 2015 08:50
por Sergio filho » Sáb Dez 05, 2015 08:50
- 1 Respostas
- 1904 Exibições
- Última mensagem por Sergio filho

Dom Dez 06, 2015 11:22
Equações
-
- Potencia de raiz
por Rodrigo Ferreira » Dom Mar 18, 2012 19:34
- 1 Respostas
- 1303 Exibições
- Última mensagem por LuizAquino

Dom Mar 18, 2012 20:30
Álgebra Elementar
-
- expressão algébrica- potência e raiz
por viniseni567 » Qua Jan 01, 2020 17:16
- 1 Respostas
- 3079 Exibições
- Última mensagem por adauto martins

Sex Jan 03, 2020 17:20
Álgebra Elementar
-
- Como calcular uma Potencia e Raiz Quadrada
por maramollica16 » Qui Fev 16, 2012 12:31
- 1 Respostas
- 2754 Exibições
- Última mensagem por MarceloFantini

Qui Fev 16, 2012 16:37
Álgebra Elementar
-
- [Série de potÊncia] Expansão de séries de potência
 por Adonias 7 » Qua Jun 01, 2016 09:05
por Adonias 7 » Qua Jun 01, 2016 09:05
- 0 Respostas
- 3686 Exibições
- Última mensagem por Adonias 7

Qua Jun 01, 2016 09:05
Sequências
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



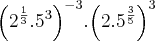

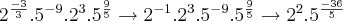
![{2}^{2}.{5}^{\frac{-36}{5}} \rightarrow 4.\frac{1}{{5}^{\frac{36}{5}}} \rightarrow \frac{4}{\sqrt[5]{{5}^{36}}} {2}^{2}.{5}^{\frac{-36}{5}} \rightarrow 4.\frac{1}{{5}^{\frac{36}{5}}} \rightarrow \frac{4}{\sqrt[5]{{5}^{36}}}](/latexrender/pictures/adbed621980776983f63a3618e1819ae.png)



 .
.



