 admite mais de uma solução se, e somente se,
admite mais de uma solução se, e somente se,  é igual a:
é igual a:Resposta: +-


 admite mais de uma solução se, e somente se,
admite mais de uma solução se, e somente se,  é igual a:
é igual a:









Douglasm escreveu:Que é equivalente ao seguinte sistema homogêneo:
Para que esse sistema admita mais de uma solução, ele deverá ser possível e indeterminado. Conseqüentemente:
Para que esse determinante seja zero, é necessário que:
![\lambda=\pm\sqrt[]{11} \lambda=\pm\sqrt[]{11}](/latexrender/pictures/2a3636cc9cb43128f726edf287c62339.png) o sistema homogêneo deve ser da seguinte forma:
o sistema homogêneo deve ser da seguinte forma:
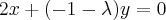
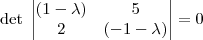

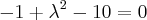


![\lambda=\pm\sqrt[]{11} \lambda=\pm\sqrt[]{11}](/latexrender/pictures/2a3636cc9cb43128f726edf287c62339.png)

Voltar para Matrizes e Determinantes
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)