 por JoaoGabriel » Sáb Set 04, 2010 10:21
por JoaoGabriel » Sáb Set 04, 2010 10:21
Bom pessoal creio que para vocês, mestres em matemática, este problema seja absurdamente simples , porém eu não consigo chegar na resposta certo.
O enunciado diz que o gráfico mostra uma função
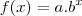
e o gráfico representa a inflação de um país . Ele pede a taxa de inflação no quarto ano (f(4)).

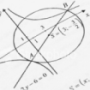
O gráfico está ruim pois foi feito no PAINT. Só para constar, a "reta" corta o eixo Y no 960.
Aí vem minha principal dúvida:
Temos os pontos (0,960). Então
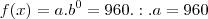
Substituindo em outros pontos ( 7 , 7,5 ), eu encontro um resultado absurdo.
PS: A resposta é 30%.
Onde está meu erro? Qual é a maneira correta de se fazer?
Obrigado
-
JoaoGabriel
- Usuário Ativo

-
- Mensagens: 19
- Registrado em: Qua Ago 18, 2010 16:05
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Estudando para Engenharia Aeroespacial
- Andamento: cursando
 por Douglasm » Sáb Set 04, 2010 11:08
por Douglasm » Sáb Set 04, 2010 11:08
Bom João, é simples, veja só:

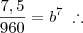
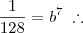

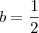
Logo:
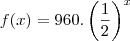
Fazendo
f(4):

Creio que haja algum erro no gabarito, ou talvez ele estivesse pedindo
f(5), que resultaria nos
30%.
-

Douglasm
- Colaborador Voluntário

-
- Mensagens: 270
- Registrado em: Seg Fev 15, 2010 10:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por JoaoGabriel » Sáb Set 04, 2010 11:19
por JoaoGabriel » Sáb Set 04, 2010 11:19
Eu entendi Douglas, obrigado. Meu maior problema foi quando cheguei na parte de
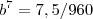
pois achei complicado calcular a raíz sétima de 7,5/960. Bom , é possível que haja mesmo erro de gabarito. Quinta Feira terei aula de álgebra e pedirei ao professor que resolva tal questão. Veremos se tem tal erro. Obrigado.
-

JoaoGabriel
- Usuário Ativo

-
- Mensagens: 19
- Registrado em: Qua Ago 18, 2010 16:05
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Estudando para Engenharia Aeroespacial
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Função exponencial] Exercício sobre função exponencial
por fff » Ter Jan 07, 2014 17:51
- 3 Respostas
- 4067 Exibições
- Última mensagem por fff

Qua Jan 08, 2014 06:47
Funções
-
- [Desigualdade] entre função exponencial e função potência
por VitorFN » Sex Mai 26, 2017 15:18
- 1 Respostas
- 5738 Exibições
- Última mensagem por adauto martins

Sex Jul 07, 2017 12:17
Álgebra Elementar
-
- [função exponencial] Exprimir em função de x
por fff » Ter Jan 07, 2014 12:02
- 2 Respostas
- 3125 Exibições
- Última mensagem por fff

Ter Jan 07, 2014 13:23
Funções
-
- funçao exponencial ITA
por zeramalho2004 » Dom Jun 28, 2009 19:55
- 3 Respostas
- 5108 Exibições
- Última mensagem por Marcampucio

Seg Jun 29, 2009 15:23
Funções
-
- Função Exponencial
por Aline » Seg Jun 29, 2009 18:59
- 3 Respostas
- 5899 Exibições
- Última mensagem por Cleyson007

Qua Jul 01, 2009 22:59
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
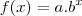 e o gráfico representa a inflação de um país . Ele pede a taxa de inflação no quarto ano (f(4)).
e o gráfico representa a inflação de um país . Ele pede a taxa de inflação no quarto ano (f(4)).
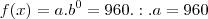



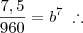
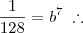

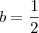
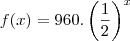


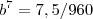 pois achei complicado calcular a raíz sétima de 7,5/960. Bom , é possível que haja mesmo erro de gabarito. Quinta Feira terei aula de álgebra e pedirei ao professor que resolva tal questão. Veremos se tem tal erro. Obrigado.
pois achei complicado calcular a raíz sétima de 7,5/960. Bom , é possível que haja mesmo erro de gabarito. Quinta Feira terei aula de álgebra e pedirei ao professor que resolva tal questão. Veremos se tem tal erro. Obrigado.

 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.