"Prove que
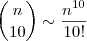 ",
",mas não me recordo o que significa este "til" entre as duas equações.
E quanto ao logaritmo neperiano: o que é o
 , não o valor, mas sim o que ele significa, como chegamos a ele, e também, como se "resolve" algo do tipo
, não o valor, mas sim o que ele significa, como chegamos a ele, e também, como se "resolve" algo do tipo 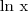 .
.Alguém poderia me ajudar com estas dúvidas?
Desde já, agradeço muito.


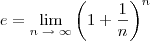


 .
.



