

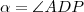 ,
,  e
e  .
. pertence à reta
pertence à reta  , ou seja
, ou seja 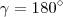 , e daí fica fácil definir o valor de
, e daí fica fácil definir o valor de  usando a soma dos ângulos internos do quadrilátero
usando a soma dos ângulos internos do quadrilátero  (que é
(que é  ) , uma vez que o ângulo
) , uma vez que o ângulo 
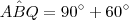 (afinal, ele é resultante da soma de um vértice do quadrado e do triângulo equilátero).
(afinal, ele é resultante da soma de um vértice do quadrado e do triângulo equilátero). está sobre
está sobre  ? Bastaria apenas usar a soma dos ângulos internos do pentágono
? Bastaria apenas usar a soma dos ângulos internos do pentágono 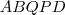 e deixar
e deixar  ,
,  e
e  como incógnitas, afim de achar a soma dos três ângulos.
como incógnitas, afim de achar a soma dos três ângulos.Usuários navegando neste fórum: Nenhum usuário registrado e 11 visitantes