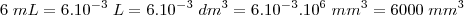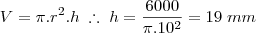por Carolziiinhaaah » Qui Set 02, 2010 14:50
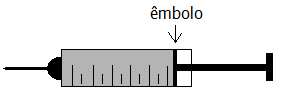
A figura abaixo representa uma seringa no formato de um cilindro circular reto, cujo êmbolo tem 20mm de diâmetro.
Esta seringa está completamente cheia de um medicamento e é usada para injetar doses de 6 ml desse medicamento.
Com basse nessas informações, determine quantos milímetros o êmbolo se desloca no interior da seinga ao ser injetada uma dose.
-
Carolziiinhaaah
- Usuário Parceiro
-
- Mensagens: 77
- Registrado em: Sex Mai 28, 2010 14:12
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
por Douglasm » Qui Set 02, 2010 18:19
Bom, você tem um volume de:
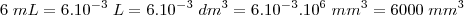
Você tem um cilindro de raio 10 mm e altura desconhecida:
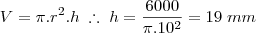
E é isso ai!
-
Douglasm
- Colaborador Voluntário
-
- Mensagens: 270
- Registrado em: Seg Fev 15, 2010 10:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Geometria Espacial
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30
Então, o exercicio pede para encontrar
.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:
Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):
Somando a primeira e a segunda equação:
Finalmente:
Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
