 por cristina » Seg Ago 30, 2010 10:21
por cristina » Seg Ago 30, 2010 10:21
Olá pessoal se alguem puder me ajudar agradeço.
Quando necessecitamos calcular a quantidade de subconjuntos possiveis de um conjunto, pode-se utilizar a equação num. [Partes (S)] =

para determinar esse numero, onde NE é o numero de elementos do conjunto S. Supondo que você deseje selecionar uma dupla de seguranças sendo sempre um do sexo masculino e o outro feminino, determine quantas duplas possiveis você poderá compor para eleborar uma escala de trabalho, sendo que você conta com o conjunto das seguintes pessoas para trabalhar: {Ana, Paulo, Mariana, Teresa, Roberto}
-
cristina
- Usuário Parceiro

-
- Mensagens: 82
- Registrado em: Qua Set 02, 2009 17:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura/ matematica
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Conjuntos] Confusão em teoria dos conjuntos numa questão.
 por Debora Bruna » Seg Jan 11, 2016 17:44
por Debora Bruna » Seg Jan 11, 2016 17:44
- 1 Respostas
- 8838 Exibições
- Última mensagem por DanielFerreira

Sáb Jan 23, 2016 16:44
Conjuntos
-
- [Conjuntos] Dúvida sobre conjuntos vazios
por ALPC » Qui Set 18, 2014 18:28
- 5 Respostas
- 6409 Exibições
- Última mensagem por adauto martins

Seg Set 22, 2014 15:44
Conjuntos
-
- [conjuntos]numeros racionais e conjuntos
por fenixxx » Ter Fev 28, 2012 21:35
- 3 Respostas
- 4724 Exibições
- Última mensagem por DanielFerreira

Sex Mar 02, 2012 00:04
Álgebra Elementar
-
- [Conjuntos] Problema de conjuntos com porcentagem
por Tibes » Qui Jan 31, 2013 14:29
- 1 Respostas
- 7954 Exibições
- Última mensagem por young_jedi

Sex Fev 01, 2013 12:39
Conjuntos
-
- [Conjuntos] Conjuntos e geometria plana
por bencz » Dom Mar 03, 2013 12:58
- 3 Respostas
- 11198 Exibições
- Última mensagem por maison_souza

Sex Nov 14, 2014 13:15
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 para determinar esse numero, onde NE é o numero de elementos do conjunto S. Supondo que você deseje selecionar uma dupla de seguranças sendo sempre um do sexo masculino e o outro feminino, determine quantas duplas possiveis você poderá compor para eleborar uma escala de trabalho, sendo que você conta com o conjunto das seguintes pessoas para trabalhar: {Ana, Paulo, Mariana, Teresa, Roberto}
para determinar esse numero, onde NE é o numero de elementos do conjunto S. Supondo que você deseje selecionar uma dupla de seguranças sendo sempre um do sexo masculino e o outro feminino, determine quantas duplas possiveis você poderá compor para eleborar uma escala de trabalho, sendo que você conta com o conjunto das seguintes pessoas para trabalhar: {Ana, Paulo, Mariana, Teresa, Roberto}

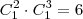




 , avisa que eu resolvo.
, avisa que eu resolvo.

