 por Balanar » Dom Ago 29, 2010 03:57
por Balanar » Dom Ago 29, 2010 03:57
Os pontos P e Q pertencem ao interior do segmento AB e estão de um mesmo lado do seu ponto médio. P divide AB na razão 2/3 e Q divide AB na razão 3/4 . Se PQ=2cm, calcule AB.
Resposta:
70 cm
To tendo dificuldade de montar o segmento, o exercício está na parte que envolve razão da secção interna e externa.
Por favor detalhe principalmente como você monto o segmento,caso tenha conseguido fazer.
Grato desde já.
To tendo dificuldades para cocnseguir montar o segmento correto, o mais difícil e montar o segmento de forma correta (to tentando fazer isso)
Eu tentei o segunite...
A.......................P............Q...............M.............B
Minha interpretação ta sendo essa mas não ta dando gabarito.
Se poderem ajudar grato desde já.
Abraços
-
Balanar
- Usuário Parceiro

-
- Mensagens: 72
- Registrado em: Qua Dez 03, 2008 07:18
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Douglasm » Dom Ago 29, 2010 15:55
por Douglasm » Dom Ago 29, 2010 15:55

- segmento.JPG (6.94 KiB) Exibido 8306 vezes
Acho que o desenho que fiz já é bastante elucidativo, mas acompanhe:
- Chamaremos o comprimento de
AB de
"x";
- Se
P divide o segmento
AB na proporção
2/3, logo
P divide o segmento
AB em dois segmentos menores,
2/5 x e
3/5 x.
- Analogamente,
Q divide o segmento
AB em dois segmentos medindo
3/7 x e
4/7 x, respectivamente.
Como podemos observar no desenho:

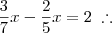
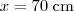
-

Douglasm
- Colaborador Voluntário

-
- Mensagens: 270
- Registrado em: Seg Fev 15, 2010 10:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Balanar » Dom Ago 29, 2010 17:15
por Balanar » Dom Ago 29, 2010 17:15
Muito bom a resposta vlw.
-
Balanar
- Usuário Parceiro

-
- Mensagens: 72
- Registrado em: Qua Dez 03, 2008 07:18
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Balanar » Dom Ago 29, 2010 18:33
por Balanar » Dom Ago 29, 2010 18:33
Como você essa figura? Você uso algum programa?
Como eu poderia fazer uma figura semelhante a essa?
Aguardo resposta.
Grato desde já.
-
Balanar
- Usuário Parceiro

-
- Mensagens: 72
- Registrado em: Qua Dez 03, 2008 07:18
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Douglasm » Dom Ago 29, 2010 19:14
por Douglasm » Dom Ago 29, 2010 19:14
Bom, eu só usei o Paint. xD
-

Douglasm
- Colaborador Voluntário

-
- Mensagens: 270
- Registrado em: Seg Fev 15, 2010 10:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Equação da Reta] Bissetriz interna e externa
por Marcos_Mecatronica » Sex Mai 17, 2013 21:48
- 1 Respostas
- 2964 Exibições
- Última mensagem por Marcos_Mecatronica

Ter Mai 21, 2013 21:09
Geometria Analítica
-
- Bissetriz Interna e Bissetriz Externa
por sauloandrade » Seg Nov 05, 2012 18:13
- 0 Respostas
- 2082 Exibições
- Última mensagem por sauloandrade

Seg Nov 05, 2012 18:13
Geometria Analítica
-
- Circunferência inscrita numa secção circular
 por Guga1981 » Ter Out 17, 2017 19:14
por Guga1981 » Ter Out 17, 2017 19:14
- 1 Respostas
- 3310 Exibições
- Última mensagem por Guga1981

Ter Out 17, 2017 19:16
Geometria Plana
-
- (GEOMETRIA PLANA) Area total externa - Planificação Sólid
 por gusavancini » Qui Ago 18, 2016 12:16
por gusavancini » Qui Ago 18, 2016 12:16
- 0 Respostas
- 4087 Exibições
- Última mensagem por gusavancini

Qui Ago 18, 2016 12:16
Geometria Plana
-
- [Triângulo retângulo] Bissetriz interna
por Ricardo MB » Seg Jul 21, 2014 22:44
- 0 Respostas
- 2056 Exibições
- Última mensagem por Ricardo MB

Seg Jul 21, 2014 22:44
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



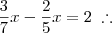
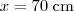



 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.