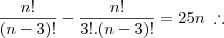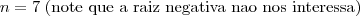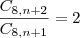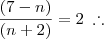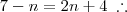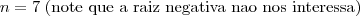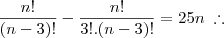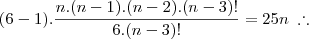por cristina » Qui Ago 26, 2010 14:13
por cristina » Qui Ago 26, 2010 14:13
Olá estou com duvida neste exercicio.
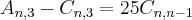
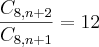
Se alguem puder me ajudar agradeço
-
cristina
- Usuário Parceiro

-
- Mensagens: 82
- Registrado em: Qua Set 02, 2009 17:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura/ matematica
- Andamento: cursando
 por DanielRJ » Qui Ago 26, 2010 15:49
por DanielRJ » Qui Ago 26, 2010 15:49
cristina escreveu:Olá estou com duvida neste exercicio.
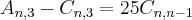
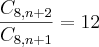
Se alguem puder me ajudar agradeço
Olá amiga a segunda eu consegui fazer vo demonstrar para voce:
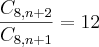
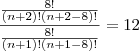
corta 8! de cima com o debaixo fica assim.

desenvolve (n+2) e (n-6) para poder cortar em baixo.
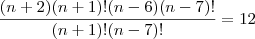
corta (n+1) e (n-7)!
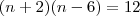
faz a distributiva!


faz baskara e acha o N!! valeu depois eu resolvo a outra.
-

DanielRJ
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Sex Ago 20, 2010 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por cristina » Qui Ago 26, 2010 16:50
por cristina » Qui Ago 26, 2010 16:50
Obrigada pela dica, onde é 12 coloquei errado é 2, porém nao consigo achar a raiz quadrada, não dá certo.
-
cristina
- Usuário Parceiro

-
- Mensagens: 82
- Registrado em: Qua Set 02, 2009 17:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura/ matematica
- Andamento: cursando
 por DanielRJ » Qui Ago 26, 2010 19:34
por DanielRJ » Qui Ago 26, 2010 19:34
cristina escreveu:Obrigada pela dica, onde é 12 coloquei errado é 2, porém nao consigo achar a raiz quadrada, não dá certo.
Oi amiga essa questão é de concurso? tem resposta?
porque eu tambem não consegui achar o valor de n não. vamos esperar uma almar boa ajudar agente.. mas as conta em cima estão tudo certinho ok?
sobre a primera questão que voce postou ela é um pouco trabalhosa consegui fazer mas vai demorar pra min fazer um latex dela então aguarda ai vlw .

-

DanielRJ
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Sex Ago 20, 2010 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por cristina » Qui Ago 26, 2010 19:43
por cristina » Qui Ago 26, 2010 19:43
Oi amigo, já tentei de tudo tbem e não consegui, as alternativas que tenho são:
a) 5
b) 6
c) 1
d) 7
e) 9
-
cristina
- Usuário Parceiro

-
- Mensagens: 82
- Registrado em: Qua Set 02, 2009 17:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura/ matematica
- Andamento: cursando
 por DanielRJ » Qui Ago 26, 2010 20:21
por DanielRJ » Qui Ago 26, 2010 20:21
cristina escreveu:Oi amigo, já tentei de tudo tbem e não consegui, as alternativas que tenho são:
a) 5
b) 6
c) 1
d) 7
e) 9
vo levar ela para um professor tentei substituir umas das opçoes no lugar de N para ver se zera a equação mas não deu.
-

DanielRJ
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Sex Ago 20, 2010 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por DanielRJ » Qui Ago 26, 2010 22:10
por DanielRJ » Qui Ago 26, 2010 22:10
Douglas é igual a 12 graças a você percebi que botei a formula na ordem errada! vo postar a resolução:
Editado pela última vez por
DanielRJ em Qui Ago 26, 2010 22:36, em um total de 1 vez.
-

DanielRJ
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Sex Ago 20, 2010 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Douglasm » Qui Ago 26, 2010 22:32
por Douglasm » Qui Ago 26, 2010 22:32
Em seu segundo post, Cristina afirmou ter errado, que na verdade a segunda expressão é igual a 2. Veja só:
cristina escreveu:Obrigada pela dica, onde é 12 coloquei errado é 2, porém nao consigo achar a raiz quadrada, não dá certo.
-

Douglasm
- Colaborador Voluntário

-
- Mensagens: 270
- Registrado em: Seg Fev 15, 2010 10:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por DanielRJ » Qui Ago 26, 2010 22:39
por DanielRJ » Qui Ago 26, 2010 22:39
aff. to aqui igual um troxa fazendo erradoe entao
-

DanielRJ
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Sex Ago 20, 2010 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por cristina » Sex Ago 27, 2010 00:48
por cristina » Sex Ago 27, 2010 00:48
Amigo, desulpe te incomodar mais uma vez,
não entendi em relação ao primeiro problema, da onde surgiu o 3 fatorial - 1 e de subtração pasou para multiplicação
não compreendi o seu raciocinio.
abs
-
cristina
- Usuário Parceiro

-
- Mensagens: 82
- Registrado em: Qua Set 02, 2009 17:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura/ matematica
- Andamento: cursando
 por cristina » Sex Ago 27, 2010 11:37
por cristina » Sex Ago 27, 2010 11:37
Obrigada
-
cristina
- Usuário Parceiro

-
- Mensagens: 82
- Registrado em: Qua Set 02, 2009 17:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura/ matematica
- Andamento: cursando
Voltar para Estatística
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- (( Analise combinatória ))
por Roberta » Dom Jul 13, 2008 17:28
- 8 Respostas
- 16359 Exibições
- Última mensagem por Aparecida

Sáb Mai 05, 2012 00:07
Estatística
-
- Análise Combinatória
por Rejane Sampaio » Sex Set 12, 2008 23:20
- 4 Respostas
- 12544 Exibições
- Última mensagem por Neilson

Ter Mai 01, 2012 01:23
Estatística
-
- Análise Combinatória
por Rejane Sampaio » Sex Set 12, 2008 23:26
- 2 Respostas
- 8470 Exibições
- Última mensagem por Rejane Sampaio

Seg Set 15, 2008 10:08
Estatística
-
- Análise Combinatória
por Rejane Sampaio » Qua Set 17, 2008 15:52
- 3 Respostas
- 7921 Exibições
- Última mensagem por Rejane Sampaio

Qui Set 25, 2008 10:43
Estatística
-
- Análise Combinatória
por Rejane Sampaio » Qua Set 17, 2008 15:56
- 2 Respostas
- 6621 Exibições
- Última mensagem por Rejane Sampaio

Seg Set 22, 2008 11:27
Estatística
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
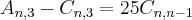
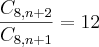

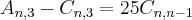
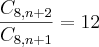

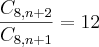
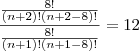 corta 8! de cima com o debaixo fica assim.
corta 8! de cima com o debaixo fica assim. desenvolve (n+2) e (n-6) para poder cortar em baixo.
desenvolve (n+2) e (n-6) para poder cortar em baixo.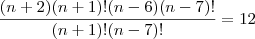 corta (n+1) e (n-7)!
corta (n+1) e (n-7)!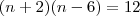 faz a distributiva!
faz a distributiva!
 faz baskara e acha o N!! valeu depois eu resolvo a outra.
faz baskara e acha o N!! valeu depois eu resolvo a outra.