Para cada inteiro
 ,
, é o numero de divisores positivos de x e g(x) é o resto da divisão de x por 5. Então
é o numero de divisores positivos de x e g(x) é o resto da divisão de x por 5. Então 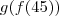 é:
é:A resposta é 1

 ,
, é o numero de divisores positivos de x e g(x) é o resto da divisão de x por 5. Então
é o numero de divisores positivos de x e g(x) é o resto da divisão de x por 5. Então 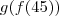 é:
é:
 é o número de divisores de x, então
é o número de divisores de x, então 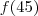 é o número de divisores de 45.
é o número de divisores de 45.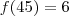
 é o resto da divisão de x por 5. Portanto,
é o resto da divisão de x por 5. Portanto, 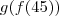 é a mesma coisa que
é a mesma coisa que 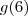 , e 6 divido por 5 tem resto 1.
, e 6 divido por 5 tem resto 1.

Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante

 .
.



