 por jose henrique » Seg Ago 16, 2010 12:31
por jose henrique » Seg Ago 16, 2010 12:31
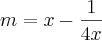
![Y=\sqrt[]{1+{m}^{2}} Y=\sqrt[]{1+{m}^{2}}](/latexrender/pictures/d698c49a12f0e71e70749efdea4e5e97.png)
x pertence ao conjunto dos números inteiros positivos excluído o zero.
eu fatorei e acabou resultando numa equação do 2 que resultou no resultado y=
![\frac{-4-+\sqrt[]{160}}{72} \frac{-4-+\sqrt[]{160}}{72}](/latexrender/pictures/48c9794247feacd98b3c68b9c8c99945.png)
pois acredito ques errei em algum lugar, pois difere do gabarito
-
jose henrique
- Colaborador Voluntário

-
- Mensagens: 129
- Registrado em: Qui Ago 12, 2010 20:32
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: outros
- Andamento: formado
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- números naturais
por jose henrique » Dom Ago 15, 2010 15:24
- 2 Respostas
- 1701 Exibições
- Última mensagem por jose henrique

Seg Ago 16, 2010 10:40
Álgebra Elementar
-
- números naturais
por jose henrique » Seg Ago 16, 2010 11:44
- 0 Respostas
- 1175 Exibições
- Última mensagem por jose henrique

Seg Ago 16, 2010 11:44
Álgebra Elementar
-
- números naturais
por jose henrique » Ter Ago 24, 2010 23:49
- 3 Respostas
- 2188 Exibições
- Última mensagem por MarceloFantini

Qua Ago 25, 2010 13:13
Álgebra Elementar
-
- Conjunto dos números naturais
por adriano rodrigues » Dom Dez 12, 2010 18:24
- 3 Respostas
- 3174 Exibições
- Última mensagem por adriano rodrigues

Ter Dez 14, 2010 19:44
Álgebra Elementar
-
- [Desafios com números naturais]
por mar+ci+lene » Ter Mai 29, 2012 22:24
- 1 Respostas
- 2840 Exibições
- Última mensagem por Russman

Ter Mai 29, 2012 23:00
Desafios Fáceis
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
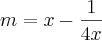
![Y=\sqrt[]{1+{m}^{2}} Y=\sqrt[]{1+{m}^{2}}](/latexrender/pictures/d698c49a12f0e71e70749efdea4e5e97.png)
![\frac{-4-+\sqrt[]{160}}{72} \frac{-4-+\sqrt[]{160}}{72}](/latexrender/pictures/48c9794247feacd98b3c68b9c8c99945.png)

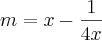
![Y=\sqrt[]{1+{m}^{2}} Y=\sqrt[]{1+{m}^{2}}](/latexrender/pictures/d698c49a12f0e71e70749efdea4e5e97.png)
![\frac{-4-+\sqrt[]{160}}{72} \frac{-4-+\sqrt[]{160}}{72}](/latexrender/pictures/48c9794247feacd98b3c68b9c8c99945.png)

