 por Padoan » Qua Ago 11, 2010 18:53
por Padoan » Qua Ago 11, 2010 18:53
Os números A e B são tais que AB = 2³ . 3² . 5 e a/b = 2/5. O máximo divisor comum de a e b é:
a)10 b)8 c)6 d)4
Nesse exercicio eu consegui chegar a resposta letra d) 4, com a = 8 e b = 20, correto?
Já esse, foi um que eu agarrei:
Considerando-se todas as divisões de inteiros positivos por 30 em que o resto é igual ao cubo do quociente, podemos afirmar que a soma dos possíveis quocientes é:
a)6 b)5 c)4 d)3
N -> números naturais inteiros e positivos
q -> quociente
N =30 . q³ + q
N=30 . 2q³
E aí eu nao sei mais... eu teria que ir por tentativas?
Qualquer ajuda seria bem vinda D:
-
Padoan
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Qui Fev 11, 2010 14:34
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Molina » Qui Ago 12, 2010 16:51
por Molina » Qui Ago 12, 2010 16:51
Boa tarde.
Padoan escreveu:Os números A e B são tais que AB = 2³ . 3² . 5 e a/b = 2/5. O máximo divisor comum de a e b é:
a)10 b)8 c)6 d)4
Nesse exercicio eu consegui chegar a resposta letra d) 4, com a = 8 e b = 20, correto?
Neste exercício a mesma solução deu diferente. Tente comparar com a sua e ver qual de nós está se equivocando em algum momento:
 (equação 1)
(equação 1)e
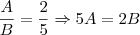 (equação 2)
(equação 2)Substituindo a equação 1 na equação 2, temos:
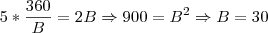
Voltando e substiuindo B na equação 1 ou 2, temos

E o


Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por alexandre32100 » Sex Ago 13, 2010 01:30
por alexandre32100 » Sex Ago 13, 2010 01:30
-
alexandre32100
-
 por Padoan » Sex Ago 13, 2010 23:10
por Padoan » Sex Ago 13, 2010 23:10
Eu errei ao passar pro papel, eu li no exercicio e passei pra folha como ab = 2³ . 2² . 5, ao invés do 2³... então fico a = 160/b, daí por isso achei resposta diferente. Falta de atenção mesmo...
Mas muito obrigado pela ajuda!
-
Padoan
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Qui Fev 11, 2010 14:34
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Duvida em Questão de (EDO)
por sys_ » Sex Abr 10, 2009 19:06
- 2 Respostas
- 2318 Exibições
- Última mensagem por nakagumahissao

Seg Ago 17, 2015 13:04
Cálculo: Limites, Derivadas e Integrais
-
- Dúvida em questão de P.A.
por mushthielv » Seg Ago 17, 2009 12:18
- 3 Respostas
- 7251 Exibições
- Última mensagem por DanielFerreira

Dom Ago 23, 2009 12:59
Progressões
-
- Dúvida na questão
por GABRIELA » Ter Set 01, 2009 17:17
- 2 Respostas
- 6164 Exibições
- Última mensagem por Molina

Ter Set 01, 2009 23:28
Matrizes e Determinantes
-
- duvida na questão
por GABRIELA » Qua Set 30, 2009 17:06
- 10 Respostas
- 6666 Exibições
- Última mensagem por GABRIELA

Qua Set 30, 2009 22:42
Geometria Analítica
-
- Duvida na questão
por igorcalfe » Qua Nov 03, 2010 16:21
- 2 Respostas
- 1638 Exibições
- Última mensagem por igorcalfe

Qua Nov 03, 2010 17:16
Logaritmos
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



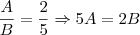
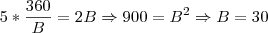




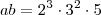 e
e 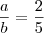 basta fazer a subtituição:
basta fazer a subtituição:
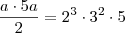


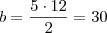
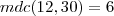 , letra
, letra  , mesma conclusão do Molina.
, mesma conclusão do Molina.