Bom, primeiramente, temos que considerar o tempo que leva-se na ida (em que considerarei que o vento está a favor) e o tempo que se leva na volta (quando o vento está contra o movimento do avião). Depois disso, basta somarmos os tempos (pois já temos o tempo total de 4 hrs) e teremos
d em função de
v. Comecemos:
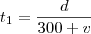

Somando-os:
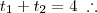

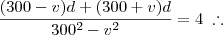
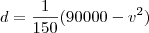
Sobre a letra b, o que se pede é a distância máxima que o avião percorerá, não o valor de
v nesse caso. Só de observar a função acima, vemos que
d é máximo para
v = 0 e que é igual a 600km.
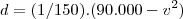


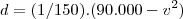


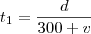

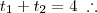

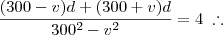
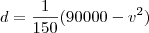


 .
.
 :
: