Stephanie escreveu:Eu não faço a minima ideia de o que é o termo médio e o meu desenvolvimento está errado! por favor me ajudem!!
No desenvolvimento de (x+y) [elevado a n ] a diferença entre os coeficientes da 3º e do 2º termo é igual a 54. Podemos afirmar que o temro médio é o :
a- 3º
b- 4º
c- 5º
d- 6º
e- 7º
Obrigada
Bom dia.
Primeiramente,
Termo Central ou Médio é aquele que fica no meio, se o desenvolvimento for de grau par.
Por exemplo, em
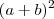
, onde

, o grau é par. Desenvolvendo este binômio temos que:
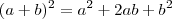
, ou seja, o termo médio é o
2ab, por estar justamente no CENTRO do desenvolvimento do binômio.
Considerando agora um binômio genérico, ou seja,

, pela fórmula geral do Binômio de Newton, temos que:
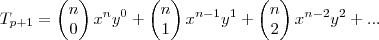
Como a questão fala em 2° e 3° termo, não precisamos dar continuidade no desenvolvimento. Os coeficientes destes termos são, respectivamente,

e

.
Seguindo o que o enunciado diz,
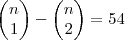
Vale lembrar que
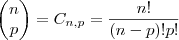
Desenvolvendo
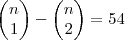
chegamos em

e

. Ficamos apenas com o valor positivo, ou seja,

.
Isso significa, que desenvolvendo agora

teremos

termos.
Basta você verificar de 1 ao 13 qual é o termo central.



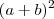 , onde
, onde  , o grau é par. Desenvolvendo este binômio temos que:
, o grau é par. Desenvolvendo este binômio temos que: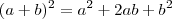 , ou seja, o termo médio é o
, ou seja, o termo médio é o  , pela fórmula geral do Binômio de Newton, temos que:
, pela fórmula geral do Binômio de Newton, temos que: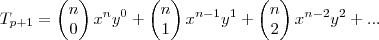
 e
e  .
.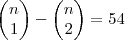
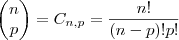
 e
e  . Ficamos apenas com o valor positivo, ou seja,
. Ficamos apenas com o valor positivo, ou seja,  teremos
teremos  termos.
termos.
