Partindo da sua equação, não dá pra chegar na derivada que você mencionou.
Usando a regra do quociente, podemos achar a sua derivada , observe :
![[ Q^6/ 2l^2]' = [6Q^5 * dQ/dL *2L^2 - Q^6*4L]/4L^4 [ Q^6/ 2l^2]' = [6Q^5 * dQ/dL *2L^2 - Q^6*4L]/4L^4](/latexrender/pictures/8bf3de57809304860a01e176c69883f8.png)
Mas queremos a derivada de [Q^6/ 2L^2 + L] ; como a derivada de " L " é igual a " 1 " , teremos :
![[ Q^6/ 2L² + L ]' = [6Q^5 * dQ/dL *2L^2 - Q^6*4L]/4L^4 + 1 [ Q^6/ 2L² + L ]' = [6Q^5 * dQ/dL *2L^2 - Q^6*4L]/4L^4 + 1](/latexrender/pictures/b700381563c9bd7884bdc5d0d6f59d20.png)
.................................x.....................................x..........................................x...............................
Lembre - se :
[ f(x)/g(x) ] = f'(x).g(x) - f(x).g'(x) / [ g(x) ] ²
.................................x.....................................x..........................................x................................
Na sua segunda questão, você precisa seguir a regra que postei acima, e assim teremos a derivada correta, pois você não pode usar a regra da potência em uma divisão. Use a regra do quociente !!!
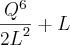
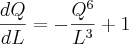

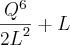
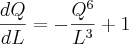


![[ Q^6/ 2l^2]' = [6Q^5 * dQ/dL *2L^2 - Q^6*4L]/4L^4 [ Q^6/ 2l^2]' = [6Q^5 * dQ/dL *2L^2 - Q^6*4L]/4L^4](/latexrender/pictures/8bf3de57809304860a01e176c69883f8.png)
![[ Q^6/ 2L² + L ]' = [6Q^5 * dQ/dL *2L^2 - Q^6*4L]/4L^4 + 1 [ Q^6/ 2L² + L ]' = [6Q^5 * dQ/dL *2L^2 - Q^6*4L]/4L^4 + 1](/latexrender/pictures/b700381563c9bd7884bdc5d0d6f59d20.png)

