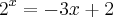
Como se calcula e qual o valor?
Obrigado desde já

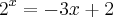

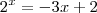 , temos:
, temos: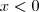 , então
, então 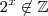 ao passo que
ao passo que  e assim a igualdade seria absurda!
e assim a igualdade seria absurda! não é solução; o que pode ser verificado trivialmente. Assim, deveremos ter
não é solução; o que pode ser verificado trivialmente. Assim, deveremos ter  o que decorre em
o que decorre em 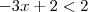 e implica:
e implica: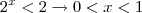 . Mas, se
. Mas, se 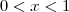 , então
, então 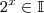 ao passo que
ao passo que 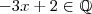 e assim a igualdade seria absurda!
e assim a igualdade seria absurda!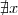 que satisfaça a equação.
que satisfaça a equação.
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante