Eu sei que essa eh uma das primeiras coisas que se aprende quando se ve essa matéria, mas, mesmo depois de já tê-la visto na escola, essa dúvida ressurgiu depois que meu prof de geometria deu como desafio ver o erro daquelas demonstrações falsas, que 'provam' coisas doidas, tipo 2 = 1, 0 = 1, ou... i² = 1.
Como eu não quero que simplesmente me digam a resposta do problema, queria tirar uma dúvida:
![$\sqrt[2]{-1} *\sqrt[2]{-1}$ $\sqrt[2]{-1} *\sqrt[2]{-1}$](/latexrender/pictures/74f8c1ef74a2bc0f8946bbba0369bd36.png) é 1 ou -1? E pq?
é 1 ou -1? E pq?É que eu pensei de duas formas:
1ª forma:
![$\sqrt[2]{-1}*\sqrt[2]{-1} = \sqrt[2]{-1 * -1} = \sqrt[2]{(-1)^2} = (-1^2)^{1/2} = -1}$ $\sqrt[2]{-1}*\sqrt[2]{-1} = \sqrt[2]{-1 * -1} = \sqrt[2]{(-1)^2} = (-1^2)^{1/2} = -1}$](/latexrender/pictures/4b536cf31308587358b59200fc0c32f5.png)
2ª forma:
![$\sqrt[2]{-1} *\sqrt[2]{-1} = \sqrt[2]{-1 * -1} = \sqrt[2]{(1} =1}$ $\sqrt[2]{-1} *\sqrt[2]{-1} = \sqrt[2]{-1 * -1} = \sqrt[2]{(1} =1}$](/latexrender/pictures/4921e0da39c6fd936d370c5e36ff0081.png)
Bem, mais uma vez desculpa se for algo muito fácil...
Mas, onde está o erro de algum desses dois raciocinios?
Agradeço desde já ^.^
E peço a compreensão de vcs =D
=* kissú



 ,
, ![\sqrt[2]{a}*\sqrt[2]{a} \neq \sqrt[2]{a*a} \sqrt[2]{a}*\sqrt[2]{a} \neq \sqrt[2]{a*a}](/latexrender/pictures/f70e9192d518c2f2be6fc04924bb72da.png)
![\sqrt[2]{-1}*\sqrt[2]{-1} = -1 \sqrt[2]{-1}*\sqrt[2]{-1} = -1](/latexrender/pictures/48c678beedbcdccee78969fb9d0f4be8.png)



 , passando por
, passando por  .
.


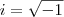 é uma definição, isto é, um atributo que foi convencionado e que, a rigor, não pode ser demonstrado.
é uma definição, isto é, um atributo que foi convencionado e que, a rigor, não pode ser demonstrado.
![i = \sqrt[]{-1} i = \sqrt[]{-1}](/latexrender/pictures/b2d69e603f696fdfb9e3f4c879ddb134.png)
 e
e 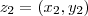 :
: