 por ckde » Qua Jul 14, 2010 12:20
por ckde » Qua Jul 14, 2010 12:20
Sejam , a,b,c, d números primos distintos e seja x um número primo que divide o número abcd.
Prove que x é diferente de a,b ,c , d.
-
ckde
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Qua Jul 14, 2010 10:23
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por MarceloFantini » Qua Jul 14, 2010 15:32
por MarceloFantini » Qua Jul 14, 2010 15:32
Essa questão é meio estranha...de onde pegou?
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por ckde » Qua Jul 14, 2010 17:39
por ckde » Qua Jul 14, 2010 17:39
De uma olimpíada de matemática. Sabe resolver?
-
ckde
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Qua Jul 14, 2010 10:23
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Molina » Qua Jul 14, 2010 21:39
por Molina » Qua Jul 14, 2010 21:39
Boa noite.
Vou fazer uma análise particular e vamos ver onde chegamos.
Sejam 2, 3, 5 e 7. Seja
x um número primo que divide o número 2357.
Nesta
página achei que este número é primo. (Há bastante coisa curiosa sobre este número, vale apena conferir).
Logo

, que é diferente dos números pegos no exemplo.
Agora não consegui ver nenhuma relação para provar que com quaisquer números que eu pegar vou obter o mesmo resultado que encontramos.
Qualquer colaboração é bem vinda!
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Douglasm » Qui Jul 15, 2010 13:30
por Douglasm » Qui Jul 15, 2010 13:30
Estava pensando nesse problema também Molina (e são bacanas estas curiosidades envolvendo 2357 =P). Mas voltando à questão, essa relação deixa de ser válida para 7532, por exemplo (é divisível por 2), sendo assim, tenho minhas dúvidas quanto a ser possível conseguir essa prova...
-

Douglasm
- Colaborador Voluntário

-
- Mensagens: 270
- Registrado em: Seg Fev 15, 2010 10:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Tom » Sex Jul 16, 2010 00:54
por Tom » Sex Jul 16, 2010 00:54
A fim de nos previnir de eventuais erros no enunciado, penso que deveríamos analisar a seguinte conjectura:
Dados os primos distintos
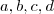
, existe um primo

, diferente dos supracitados, que divide o número

Tom
-
Tom
- Usuário Parceiro

-
- Mensagens: 75
- Registrado em: Sex Jul 02, 2010 00:42
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Automação e Controle Industrial
- Andamento: formado
 por ckde » Sáb Jul 17, 2010 13:01
por ckde » Sáb Jul 17, 2010 13:01
Desculpem, realmente ficou difícil sem usar o LaTeX... A questão tem um errinho. O certo é: seja

um número primo que divide o número

, é ab + cd e não abcd
-
ckde
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Qua Jul 14, 2010 10:23
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Douglasm » Sáb Jul 17, 2010 13:17
por Douglasm » Sáb Jul 17, 2010 13:17
Então "ab" e "cd" são produtos? Se for assim é fácil. Note que ab+cd não é divisível por nenhum deles (dito que a, b, c e d são primos). Por exemplo:

O mesmo vale para b, c e d. Logo, é evidente que, se ab+cd não é divisível por qualquer dos primos supracitados, ele é divisível por, pelo menos, um outro primo x.
-

Douglasm
- Colaborador Voluntário

-
- Mensagens: 270
- Registrado em: Seg Fev 15, 2010 10:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Molina » Sáb Jul 17, 2010 14:12
por Molina » Sáb Jul 17, 2010 14:12
Douglasm escreveu:Então "ab" e "cd" são produtos? Se for assim é fácil. Note que ab+cd não é divisível por nenhum deles (dito que a, b, c e d são primos). Por exemplo:

O mesmo vale para b, c e d. Logo, é evidente que, se ab+cd não é divisível por qualquer dos primos supracitados, ele é divisível por, pelo menos, um outro primo x.
Boa tarde, Douglas.
Acho que é isso que você colocou mesmo, pois o autor da questão criou um
novo tópico, onde diz:
ckde escreveu:Sejam , a,b,c, d números primos distintos e seja x um número primo que divide o número ab+cd.
Prove que x é diferente de a,b ,c , d.

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Tom » Sáb Jul 17, 2010 14:13
por Tom » Sáb Jul 17, 2010 14:13
ckde escreveu:Desculpem, realmente ficou difícil sem usar o LaTeX... A questão tem um errinho. O certo é: seja

um número primo que divide o número

, é ab + cd e não abcd
aff... totalmente errado

Tom
-
Tom
- Usuário Parceiro

-
- Mensagens: 75
- Registrado em: Sex Jul 02, 2010 00:42
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Automação e Controle Industrial
- Andamento: formado
 por ckde » Sáb Jul 17, 2010 22:23
por ckde » Sáb Jul 17, 2010 22:23
Agora a questão está correta... Mas, do jeito do Douglas, não está provado o que foi pedido... Mas a idéia foi boa...
-
ckde
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Qua Jul 14, 2010 10:23
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Tom » Sáb Jul 17, 2010 22:29
por Tom » Sáb Jul 17, 2010 22:29
Ckde, como é a pergunta no fim das contas?
Tom
-
Tom
- Usuário Parceiro

-
- Mensagens: 75
- Registrado em: Sex Jul 02, 2010 00:42
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Automação e Controle Industrial
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Números primos
 por mony0771 » Qui Abr 23, 2009 10:54
por mony0771 » Qui Abr 23, 2009 10:54
- 2 Respostas
- 4103 Exibições
- Última mensagem por mony0771

Qui Abr 23, 2009 15:28
Álgebra Elementar
-
- Numeros Primos
por Neperiano » Sex Abr 24, 2009 20:15
- 6 Respostas
- 5718 Exibições
- Última mensagem por Neperiano

Sáb Abr 25, 2009 10:23
Problemas do Cotidiano
-
- Fatores primos
por GMAT2010 » Qua Fev 03, 2010 20:59
- 3 Respostas
- 1855 Exibições
- Última mensagem por GMAT2010

Sáb Fev 06, 2010 07:40
Funções
-
- Números Primos
por Abelardo » Qua Mar 09, 2011 21:38
- 1 Respostas
- 3056 Exibições
- Última mensagem por Abelardo

Qua Mar 09, 2011 21:41
Álgebra Elementar
-
- OBM - Números primos
por Abelardo » Sáb Mar 12, 2011 16:54
- 4 Respostas
- 4682 Exibições
- Última mensagem por Abelardo

Dom Mar 13, 2011 13:26
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




 , que é diferente dos números pegos no exemplo.
, que é diferente dos números pegos no exemplo.

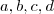 , existe um primo
, existe um primo  , diferente dos supracitados, que divide o número
, diferente dos supracitados, que divide o número 

 um número primo que divide o número
um número primo que divide o número  , é ab + cd e não abcd
, é ab + cd e não abcd




um número primo que divide o número
, é ab + cd e não abcd









